Cho số phức z thỏa mãn (1 + z)^2 là số thực. Tập hợp điểm M biểu diễn

Câu hỏi:

Cho số phức z thỏa mãn ${(1 + z)}^{2}$ là số thực. Tập hợp điểm M biểu diễn số phức z là:

A. Đường tròn

B. Đường thẳng

C. Hai đường thẳng

D. Một điểm duy nhất

Trả lời:

Đáp án C

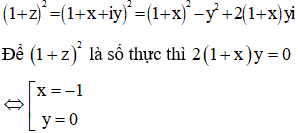
Vậy tập hợp các điểm M thỏa mãn là hai đường thẳng x = - 1 và y = 0.

Câu 1:

Tính mô đun của số phức z biết $\bar{z} = (4 - 3 i) (1 + i)$

Câu 2:

Biết rằng z là số phức có mô đun nhỏ nhất thỏa mãn $(1 - z) (\bar{z} + 2 i)$ là số thực. Số phức z là:

Câu 3:

Tìm tập hợp các điểm biểu diễn số phức z, biết rằng số phức $z^{2}$ có điểm biểu diễn nằm trên trục tung.

Câu 4:

Tập hợp các điểm trên mặt phẳng tọa độ Oxy biểu diễn số phức z thỏa mãn điều kiện: số phức $w = (z - i) (2 + i)$ là một số thuần ảo là:

Câu 5:

Cho số phức v = a + bi. Tập hợp các điểm trên mặt phẳng tọa độ Oxy biểu diễn số phức z thỏa mãn điều kiện $|z - v| = 1$ là:

Câu 6:

Tập hợp các điểm trong mặt phẳng tọa độ biểu diễn số phức z thỏa mãn điều kiện $2 |z - i| = |z - \bar{z} + 2 i|$ là hình gì?

Câu 7:

Tập hợp các điểm M biểu diễn số phức z thỏa mãn $|z - i| + |z + i| = 4$ là:

Các dạng bài tập Toán lớp 12