Cho tam giác ABC cân tại A nội tiếp đường tròn (O), AC = 5a, BC = 6a. Tính khoảng cách từ điểm O đến dây BC theo a.
Câu hỏi:
Cho tam giác ABC cân tại A nội tiếp đường tròn (O), AC = 5a, BC = 6a. Tính khoảng cách từ điểm O đến dây BC theo a.
Trả lời:
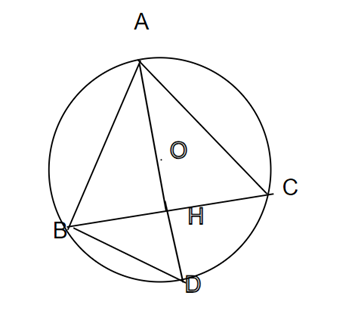
Kẻ đường kính AD sao cho A, O, D, H thẳng hàng
Vì ABC cân tại A nên AB = AC = 5a.
HB = HC = BC : 2 = 6a : 2 = 3a
Tam giác AHC vuông tại H, ta có:
Tam giác ABD nội tiếp đường tròn tâm O đường kính AD nên:
Suy ra: Tam giác ABD vuông tại B
Theo hệ thức lượng, ta có: AB2 = AH.AD
Suy ra: AD = 25a2 : 4a =
OA = OD =
Khoảng cách từ O đến BC = OH - AH – OA =

