Cho tam giác ABC cân tại A. Từ một điểm D trên đáy BC, ta vẽ đường thẳng vuông góc với BC, cắt các cạnh AB, AC lần lượt tại E, F. Vẽ các hình chữ nhật BDEH, CDFK. Chứng minh rằng A là trung t
Câu hỏi:
Cho tam giác ABC cân tại A. Từ một điểm D trên đáy BC, ta vẽ đường thẳng vuông góc với BC, cắt các cạnh AB, AC lần lượt tại E, F. Vẽ các hình chữ nhật BDEH, CDFK. Chứng minh rằng A là trung tâm điểm của HK.
Trả lời:
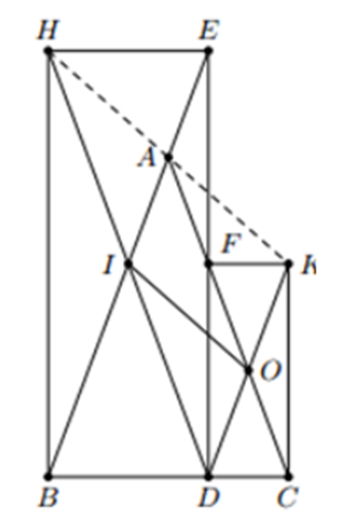
Gọi I, O lần lượt là tâm của BDEH, CDFK
Ta có:
Mà (do tam giác ABC cân tại A)
Nên:
Do đó: BE // DK, DH // CA
Suy ra: AIDO là hình bình hành
Nên: AO = ID
Mà HI = ID nên AO = HI
Lại có AO // HI và AIHO là hình bình hành nên AH // IO và AH = IO (1)
Chứng minh tương tự: AIOK là hình bình hành nên AK // io, AK = IO (2)
Từ (1) và (1): Suy ra: A, H, K thằng hàng và AH = AK.
Vậy A là trung điểm của HK.

