Cho tam giác ABC có BA = 8, AC = 9. BC = 10. Một điểm M nằm trên BC sao cho BM = 7. Tính AM.
Câu hỏi:
Cho tam giác ABC có BA = 8, AC = 9. BC = 10. Một điểm M nằm trên BC sao cho BM = 7. Tính AM.
Trả lời:
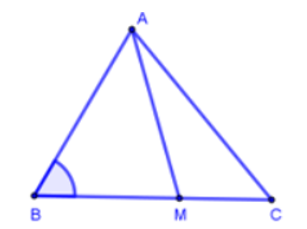
Ta có:
Áp dụng định lí cô-sin cho tam giác ABM ta có:
AM2 = AB2 + BM2 – AB.BM.cosB = .


