Cho tam giác ABC có BC = a, AC = b, Ab = c, đường phân giác AD. 1. Tính độ dài BD, DC. 2

Câu hỏi:

Cho tam giác ABC có BC = a, AC = b, Ab = c, đường phân giác AD.

1. Tính độ dài BD, DC.

2. Tia phân giác của góc B cắt AD tại I. Tính tỉ số AI : ID.

3. Cho BC bằng trung bình cộng của AB và AC, gọi G là trọng tâm của tam giác ABC. Chứng minh IG song song BC.

Trả lời:

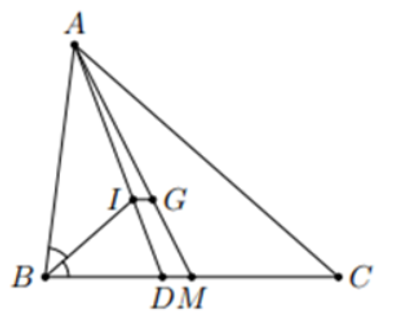
1. Vì AD là phân giác của tam giác ABC nên $\frac{D B}{A B} = \frac{D C}{A C} = \frac{D B + D C}{A B + A C} = \frac{a}{b + c}$

Vậy $D B = \frac{a c}{b + c}; D C = \frac{a b}{b + c}$

2. Vì BI là đường phân giác của tam giác BAD nên: $\frac{A I}{I D} = \frac{A B}{B D} = c : \frac{a c}{b + c} = \frac{b + c}{a}$

3. Ta có: $a = \frac{b + c}{2} \Rightarrow \frac{A I}{I D} = 2$

Mặt khác $\frac{A G}{G M} = 2$

Do đó: $\frac{A G}{G M} = \frac{A I}{I D} = 2$

Suy ra: IG // BC.

Câu 1:

Cho x + y = 15. Tìm min, max $B = \sqrt{x - 4} + \sqrt{y - 3}$

Câu 2:

Cho x,y,z là các số nguyên thỏa mãn: (x - y)(y - z)(z – x) = x + y + z. Chứng minh x + y + z chia hết cho 27.

Câu 3:

Cho x, y, z thỏa mãn đk x + y + z = a. Tìm GTNN của $P = (1 + \frac{a}{x}) (1 + \frac{a}{y}) (1 + \frac{a}{z})$

Câu 4:

Cho x + 3y – 4 = 0, tính x³ - x² + 9x²y - 9y² + 27xy² + 27y³ - 6xy

Câu 5:

Chứng minh biểu thức $A = - x^{2} + \frac{2}{3} x - 1$ luôn âm với mọi giá trị của biến

Câu 6:

Chứng minh biểu thức sau luôn âm với mọi x: –x² – 6x – 15

Câu 7:

Chứng minh với a, b dương thì $\sqrt{a + b} < \sqrt{a} + \sqrt{b}$

Câu 8:

Có tồn tại hay không một dãy gồm 2019 số tự nhiên liên tiếp mà các số đó đều là hợp số?

Các dạng bài tập Toán lớp 12