Cho tam giác ABC có đường cao AH. Trên AH, lấy các điểm K, I
Câu hỏi:
Cho tam giác ABC có đường cao AH. Trên AH, lấy các điểm K, I sao cho AK = KI = IH. Qua I, K lần lượt vẽ các đường thẳng EF//BC, MN//BC (E, M thuộc AB, F, N thuộc AC).
a) Tính \(\frac{{MN}}{{BC}};\frac{{EF}}{{BC}}\).
b) Cho biết diện tích của tam giác ABC là 90cm2. Tính diện tích tứ giác MNFE.
Trả lời:
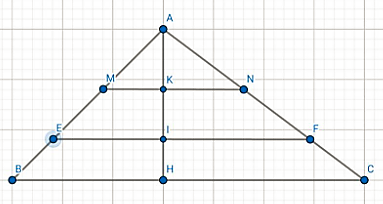
a) Theo giả thiết: MN // BC nên \(\frac{{MN}}{{BC}} = \frac{{AM}}{{AB}} = \frac{{AK}}{{AH}}\)
Mà \(AK = \frac{1}{3} \Rightarrow \frac{{MN}}{{BC}} = \frac{1}{3}\)
Lại có: EF // BC nên \(\frac{{EF}}{{BC}} = \frac{{AE}}{{AB}} = \frac{{AI}}{{AH}} = \frac{2}{3}\)
b) Ta có: SABC = \(\frac{1}{2}.AH.BC\)
SAMN = \(\frac{1}{2}.AK.MN = \frac{1}{2}.\frac{1}{3}AH.\frac{1}{3}BC = \frac{1}{9}{S_{ABC}}\)
SAEF = \(\frac{1}{2}AI.EF = \frac{1}{2}.\frac{2}{3}.AH.\frac{2}{3}BE = \frac{4}{9}{S_{ABC}}\)
SMNFE = SAFE – SAMN = \(\frac{4}{9}{S_{ABC}} - \frac{1}{9}{S_{ABC}} = \frac{1}{3}{S_{ABC}} = \frac{1}{3}.90 = 30\left( {c{m^2}} \right)\)
Vậy SMNFE = 30cm2.

