Câu hỏi:
Cho tam giác ABC có \(\widehat B = \widehat C\), gọi H là trung điểm BC. Chứng minh AH là phân giác góc \(\widehat A\).
Trả lời:
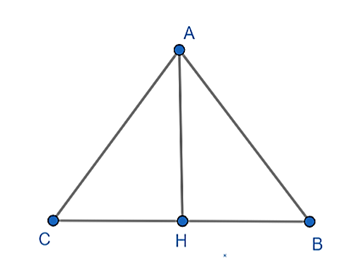
Vì \(\widehat B = \widehat C\) nên tam giác ABC cân tại A. Suy ra: AB = AC
Xét tam giác ABH và tam giác ACH có:
AB = AC
HB = HC (H là trung điểm BC)
AH chung
⇒ ∆AHB = ∆AHC
⇒ \(\widehat {HAB} = \widehat {HAC} = \frac{1}{2}\widehat {BAC}\)
Vậy AH là phân giác của \(\widehat A\).
Câu 1:
Xét xem dãy un = 3n – 1 có phải là cấp số nhân hay không? Nếu phải hãy xác định công bội.
Câu 2:
Một vé xem phim có mức giá là 60000 đồng. Trong dịp khuyến mãi cuối năm 2018, số lượng người xem phim tăng lên 45% nên tổng doanh thu cũng tăng 8,75%. Hỏi rạp phim đã giảm giá mỗi vé bao nhiêu % so với giá bán ban đầu?
Câu 6:
Câu 7:
Cho hình bình hành ABCD và O là giao điểm của AC và BD. Trên đường chéo AC lấy 2 điểm M và N sao cho AM = MN = NC
a) Chứng minh: tứ giác BMDN là hình bình hành.
b) BC cắt DN tại K. Chứng minh: N là trọng tâm của tam giác BDC.
Câu 8:
Cho a, b, m là các số tự nhiên khác 0. Biết (7a + b) chia hết cho m và (8a + b) chia hết cho m. Chứng minh rằng b cũng chia hết cho m.
