Cho hình bình hành ABCD và O là giao điểm của AC và BD
Câu hỏi:
Cho hình bình hành ABCD và O là giao điểm của AC và BD. Trên đường chéo AC lấy 2 điểm M và N sao cho AM = MN = NC
a) Chứng minh: tứ giác BMDN là hình bình hành.
b) BC cắt DN tại K. Chứng minh: N là trọng tâm của tam giác BDC.
Trả lời:
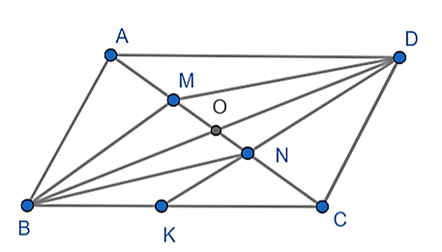
a) Theo giả thiết ta có: AM = MN = NC = \(\frac{1}{3}AC\)
Lại có: ABCD là hình bình hành nên AC và BD cắt nhau tại trung điểm O mỗi đường. Nên: OA = OC = OB = OD
Mà OA = AM + OM; OC = ON + NC
Suy ra: OM = ON hay O là trung điểm của MN
Xét tứ giác BMDN có:
O là trung điểm MN
O là trung điểm BD
Do đó: BMDN là hình bình hành
b) Ta có: ON + NC = OC
ON + \(\frac{1}{3}AC\) = \(\frac{1}{2}AC\)
ON = \(\frac{1}{6}AC\)
Suy ra: \(\frac{{ON}}{{OC}} = \frac{{\frac{1}{6}AC}}{{\frac{1}{2}AC}} = \frac{1}{3}\).
Xét tam giác BDC có: O là trung điểm BD nên CO là đường trung tuyến của BDC
Mà \(\frac{{ON}}{{OC}} = \frac{1}{3};\frac{{CN}}{{CO}} = \frac{2}{3}\)
Suy ra: N là trọng tâm của tam giác BDC.

