Cho tam giác ABC nhọn (AB < AC ) có ba đường cao AD, BE, CF cắt nhau tại H.
Câu hỏi:
Cho tam giác ABC nhọn (AB < AC ) có ba đường cao AD, BE, CF cắt nhau tại H.
a) Chứng minh: tam giác AEB đồng dạng tam giác AFC.
b) Chứng minh: AF.AB = AE.AC và tam giác AEF đồng dạng với tam giác ABC.
Trả lời:
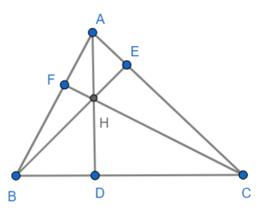
a) Xét ΔAEB vuông tại E và ΔAFC vuông tại F có
chung
Do đó: ΔAEB ∽ ΔAFC (g-g)
b) Ta có: ΔAEB ∽ ΔAFC(cmt)
nên hay AE.AC = AF.AB
Xét ΔAEF và ΔABC có
(cmt)
chung
Do đó: ΔAEF ∽ ΔABC (c-g-c).


