Cho tam giác ABC nhọn (AB < AC) có các đường cao BD và CE
Câu hỏi:
Cho tam giác ABC nhọn (AB < AC) có các đường cao BD và CE.
a, Cho góc A = 60 độ và AC = 12cm, tính AE và CE.
b, Tia DE cắt BC ở F. Chứng minh tam giác ADE đồng dạng với tam giác ABC.
c, Chứng minh FB.FC = FE.FD.
Trả lời:
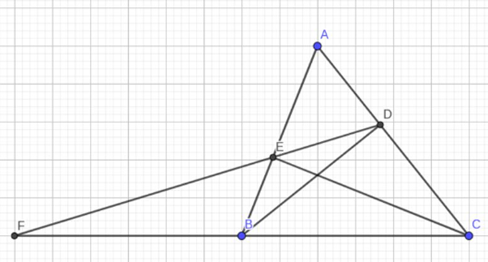
a) Ta có: \(\sin \widehat A = \frac{{CE}}{{CA}} \Rightarrow CE = AC.\sin \widehat A = 6\sqrt 3 \)
AE = \(\sqrt {A{C^2} - C{E^2}} = 6\)
b) Xét ΔADB, ΔAEC có:
Chung \(\widehat A\)
\(\widehat D = \widehat E = 90^\circ \)
⇒ ΔADB ∽ ΔAEC(g.g)
⇒ \(\frac{{AD}}{{AE}} = \frac{{AB}}{{AC}}\)
Mà \(\widehat {DAE} = \widehat {BAC}\)
⇒ ΔADE ∽ ΔABC (c.g.c)
c) Từ câu b: ΔADE ∽ ΔABC suy ra: \(\widehat {AED} = \widehat {ACB}\)
⇒ \(\widehat {FEB} = \widehat {AED} = \widehat {ACB} = \widehat {FCD}\)
Mà \(\widehat {EFB} = \widehat {DFC}\)
Xét ΔFBE và ΔFDC có:
\(\widehat {EFB} = \widehat {DFC}\)
\(\widehat {FEB} = \widehat {FCD}\)
⇒ ΔFBE ∽ ΔFDC(g.g)
⇒ \(\frac{{FB}}{{FD}} = \frac{{FE}}{{FC}}\)
⇒ FB.FC = FD.FE.

