Cho tam giác ABC vuông cân tại A có AB=AC=12. Lấy một điểm M
Câu hỏi:
Cho tam giác ABC vuông cân tại A có AB=AC=12. Lấy một điểm M thuộc cạnh huyền BC và gọi H là hình chiếu của M lên cạnh góc vuông AB. Quay tam giác AMH quanh trục là đường thẳng AB tạo thành mặt nón tròn xoay (N), hỏi thể tích V của khối nón tròn xoay (N) lớn nhất là bao nhiêu?
A.
B.
C.
D.
Trả lời:
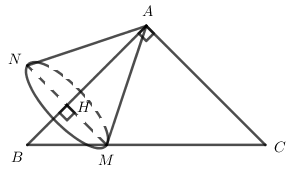
Quay tam giác vuông AMH quanh trục AB ta được khối nón có đỉnh A, bán kính đáy HM và đường cao AH, khi dó ta có thể tích của khối nón tròn xoay (N) là: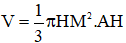 
Đặt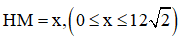 
ta có vuông cân tại H nên
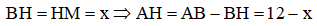
Khi đó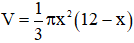 
Xét hàm số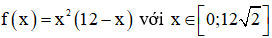 
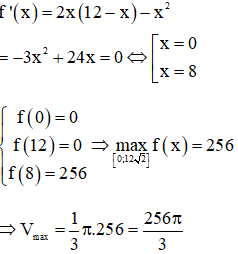
Đáp án cần chọn là: C
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Cho mặt cầu (S). Nếu (P) là mặt phẳng kính của mặt cầu (S) thì:
Xem lời giải »
Câu 2:
Khi quay hình chữ nhật ABCD quanh các cạnh nào dưới đây ta được hai hình trụ có cùng chiều cao?
Xem lời giải »
Câu 3:
Khi quay hình chữ nhật MNPQ quanh đường thẳng AB với A, B lần lượt là trung điểm của MN, PQ ta được một hình trụ có đường kính đáy:
Xem lời giải »
Câu 4:
Cho hình chữ nhật ABCD. Gọi M, N lần lượt là trung điểm các cạnh AB, CD. Quay hình chữ nhật quanh trục MN ta được hình trụ có bán kính đáy là:
Xem lời giải »
Câu 5:
Tứ diện ABCD có và góc giữa AD, BC bằng . Khi đó, bán kính mặt cầu ngoại tiếp tứ diện là:
Xem lời giải »
Câu 6:
Cho hình chóp S.ABC có SA vuông góc với đáy và . Biết bán kính mặt cầu ngoại tiếp hình chóp S.ABC bằng a. Tính độ dài cạnh BC.
Xem lời giải »
