Cho tam giác ABC vuông tại A (AB > AC) có đường cao AH. Gọi AD là phân giác của

❮ Bài trước Bài sau ❯

Câu hỏi:

Cho tam giác ABC vuông tại A (AB > AC) có đường cao AH. Gọi AD là phân giác của $\hat{H A B}$ .

a) Tính cạnh AH, AC biết HB = 18cm, HC = 8cm.

b) Chứng minh tam giác ADC cân và HD.BC = BD.DC.

c) Gọi E, F lần lượt là hình chiếu của H trên AB và AC.

Chứng minh S_AEF= S_ABC.(1 - cos²B).sin²C.

Trả lời:

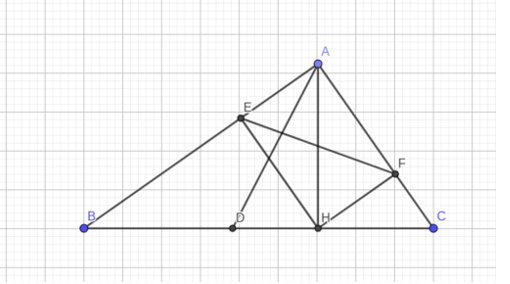
Cho tam giác ABC vuông tại A (AB > AC) có đường cao AH. Gọi AD là phân giác của (ảnh 1)

a) Ta có tam giác ABC vuông tại A, AH ⊥ BC

Nên: AH² = BH.CH = 18.8 = 144

⇒ AH = 12cm.

AC = $\sqrt{A H^{2} + H C^{2}} = 4 \sqrt{13}$

b) Vì AD là phân giác $\hat{B A H}$ ⇒ $\hat{B A D} = \hat{D A H}$

$\hat{H A C} = 90 ° - \hat{H A B} = \hat{A B H} = \hat{A B D}$

⇒ $\hat{C D A} = \hat{D A B} + \hat{D B A} = \hat{D A H} + \hat{C A H} = \hat{C A D}$

Suy ra: tam giác CAD cân tại C ⇒ CA = CD

Vì AD là phân giác $\hat{B A H}$ ⇒ $\frac{D H}{D B} = \frac{A H}{A B} = \sin B = \frac{A C}{B C}$

⇒ HD.BC = BD.AC = DB.CD

c) Ta có: HE ⊥ AB, HF ⊥ AC, AB ⊥ AC

Nên AEHF là hình chữ nhật

⇒ AH = EF

⇒ $\hat{A E F} = \hat{E A H} = \hat{B A H} = 90 ° - \hat{B} = \hat{A C B}$

Mà $\hat{E A F} = \hat{B A C}$

⇒ ∆AFE ∽ ∆ABC (g.g)

⇒ $\frac{S_{A F E}}{S_{A B C}} = {(\frac{E F}{B C})}^{2} = \frac{A H^{2}}{B C^{2}}$
Ta có: 1 – cos²B = sin²B

⇒ (1 – cos²B)sin²C = sin²Bsin²C = (sinBsinC)²

= ${(\frac{A C}{B C} . \frac{A B}{B C})}^{2} = {(\frac{A B . A C}{B C^{2}})}^{2} = {(\frac{A H . B C}{B C^{2}})}^{2} = {(\frac{A H}{B C})}^{2}$

⇒ $\frac{S_{A F E}}{S_{A B C}} = (1 - c o s^{2} B) s i n^{2} C$

⇒ S_AEF= S_ABC.(1 - cos²B).sin²C.

Xem thêm bài tập Toán có lời giải hay khác:

Câu 1:

Cho tam giác ABC có G là trọng tâm. Gọi H là chân đường cao hạ từ A sao cho $\vec{B H} = \frac{1}{3} \vec{H C}$ . Điểm M di động nằm trên BC sao cho $\vec{B M} = x \vec{B C}$ . Tìm x sao cho độ dài của $\vec{M A} + \vec{G C}$ đạt giá trị nhỏ nhất.

Xem lời giải »

Câu 2:

Cho tam giác ABC có $\hat{A} = 70 °$ , các đường phân giác BD, CE cắt nhau ở I. Tính $\hat{B I C}$

Cho tam giác ABC có góc A= 70 độ, các đường phân giác BD, CE cắt nhau ở I (ảnh 1)

Xem lời giải »

Câu 3:

Cho tam giác ABC có $\hat{C} = 90 °$ . Kẻ đường cao CH. Biết HB - HA = AC. Tính $\hat{A}, \hat{B}$ .

Xem lời giải »

Câu 4:

Cho tam giác ABC có góc C nhọn, AH và BK là hai đường cao, HK = $\sqrt{7}$ , diện tích tứ giác ABHK bằng 7 lần diện tích tam giác CHK. Khi đó bán kính đường tròn ngoại tiếp tam giác ABC bằng?

Xem lời giải »

Câu 5:

Cho tam giác ABC vuông tại A có cạnh AB = 6cm và AC = 8cm. Các đường phân giác trong và ngoài của góc B cắt đường thẳng AC lần lượt tại M và N. Tính các đoạn thẳng AM và AN.

Xem lời giải »

Câu 6:

Tam giác ABC vuông tại A có AB = 6cm, AC = 8cm. Gọi I là giao điểm các đường phân giác của tam giác.

a) Tính độ dài BI.

b) Đường vuông góc với BI tại I cắt BC tại M. Chứng minh: BM = MC.

Xem lời giải »

Câu 7:

Cho tam giác ABC vuông tại A, AC = b, AB = c. Lấy điểm M trên cạnh BC sao cho $\hat{B A M} = 30 °$ . Tính tỉ số $\frac{M B}{M C}$ .

Xem lời giải »

Câu 8:

Cho tam giác ABC vuông tại A. Kẻ AH vuông góc với BC:

a) Chứng minh: AB² + CH²= AC² + BH².