Cho tam giác ABC vuông tại A. Kẻ AH vuông góc với BC: a) Chứng minh: AB2 + CH2 = AC2 + BH2. b) Trên AB lấy E, trên AC lấy điểm F. Chứng minh: EF < BC. c) Biết AB = 6cm; AC = 8cm. Tính AH, BH,
Câu hỏi:
Cho tam giác ABC vuông tại A. Kẻ AH vuông góc với BC:
a) Chứng minh: AB2 + CH2 = AC2 + BH2.
b) Trên AB lấy E, trên AC lấy điểm F. Chứng minh: EF < BC.
c) Biết AB = 6cm; AC = 8cm. Tính AH, BH, CH.
Trả lời:
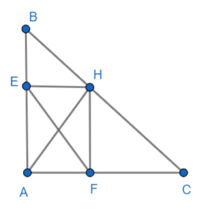
a) Áp dụng định lý Pytago vào tam giác AHB, AHC vuông có:
AB2 = BH2 + AH2 ⇒ AH2 = AB2 – BH2
AH2 = AC2 – CH2
Suy ra: AB2 – BH2 = AC2 – CH2
Hay AB2 + CH2 = AC2 + BH2
b) Ta có: EF2 = AE2 + AF2
BC2 = AB2 + AC2
AE < AB, AF < AC
Suy ra: EF2 < BC2
⇒ EF < BC.
c)
Mà AH2 = AC2 – CH2
Nên: CH =
BH = BC – CH = 10 – 6,4 = 3,6(cm).
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Cho tam giác ABC có G là trọng tâm. Gọi H là chân đường cao hạ từ A sao cho . Điểm M di động nằm trên BC sao cho . Tìm x sao cho độ dài của đạt giá trị nhỏ nhất.
Xem lời giải »
Câu 2:
Cho tam giác ABC có , các đường phân giác BD, CE cắt nhau ở I. Tính
Xem lời giải »
Câu 3:
Cho tam giác ABC có . Kẻ đường cao CH. Biết HB - HA = AC. Tính .
Xem lời giải »
Câu 4:
Cho tam giác ABC có góc C nhọn, AH và BK là hai đường cao, HK = , diện tích tứ giác ABHK bằng 7 lần diện tích tam giác CHK. Khi đó bán kính đường tròn ngoại tiếp tam giác ABC bằng?
Xem lời giải »
Câu 5:
Cho tam giác ABC vuông tại A (AB < AC), có trung tuyến AM. Kẻ MN vuông góc với AB, và MP vuông góc với AC (N thuộc AB; P thuộc AC).
a) Tứ giác ANMP là hình gì? vì sao?
b) Chứng minh: NA = NB, PA = PC và tứ giác BMPN là hình bình hành.
c) Gọi E là trung điểm của BM, F là giao điểm của AM và PN. Chứng minh tứ giác ABEF là hình thang cân.
Xem lời giải »
Câu 6:
Cho tam giác ABC vuông tại A. Về phía ngoài tam giác ABC, vẽ hai tam giác vuông cân ADB (DA = DB) và ACE (EA = EC). Gọi M là trung điểm BC, I là giao điểm của DM với AB, K là giao điểm của EM với AC. Chứng minh:
a) Ba điểm D, A, E thẳng hàng.
b) Tứ giác IAKM là hình chữ nhật.
c) Tam giác DME là tam giác vuông cân.
Xem lời giải »
Câu 7:
Tam giác ABC vuông tại A có AB = 21cm, góc C = 40°. Hãy tính các độ dài phân giác BD.
Xem lời giải »
Câu 8:
Cho tam giác ABC vuông tại A, biết AB = 6cm, . Hãy giải tam giác ABC.
Xem lời giải »



