Cho tam giác ABC vuông tại A, AH là đường cao. Biết AH/AB
Câu hỏi:
Cho tam giác ABC vuông tại A, AH là đường cao. Biết \(\frac{{AH}}{{AB}} = \frac{3}{5}\); AB = 15cm.
a) Tính HB, HC.
b) Gọi E, F lần lượt là hình chiếu của H lên AB, AC. Chứng minh: AH3 = BC.BE.CF.
Trả lời:
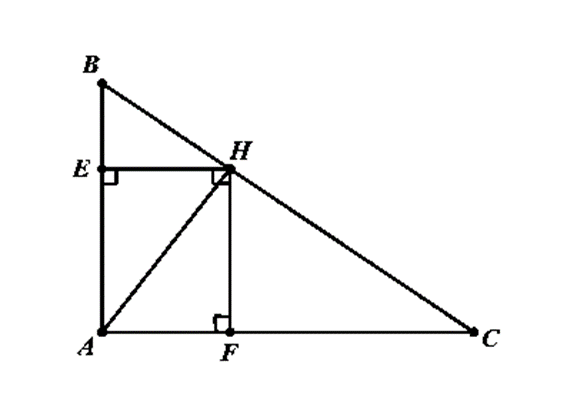
a) Ta có: \(\frac{{AH}}{{AB}} = \frac{3}{5}\), nên AH = \(\frac{3}{5}\)AC
Áp dụng hệ thức lượng trong tam giác vuông ABC có:
AB.AC = BC.AH
⇔ BC = \(\frac{{AB.AC}}{{AH}} = \frac{{AB.AC}}{{\frac{3}{5}AC}} = \frac{5}{3}AB\)
Suy ra: BC = 15.\(\frac{5}{3} = 25\)(cm)
Lại có: AB2 = BC.BH ⇒ BH = \(\frac{{A{B^2}}}{{BC}} = \frac{{{{15}^2}}}{{25}} = 9\left( {cm} \right)\)
CH = BC – BH = 25 – 9 = 16 (cm).
b) Áp dụng hệ thức lượng trong các tam giác vuông ABC, AHB, AHC ta có:
AB.AC = BC.AH ⇒ \(BC = \frac{{AB.AC}}{{AH}}\)
BH2 = AB.BE ⇒ \(BE = \frac{{B{H^2}}}{{AB}}\)
CH2 = AC.CF ⇒ \(CF = \frac{{C{H^2}}}{{AC}}\)
Khi đó: \(BE.CF = \frac{{B{H^2}}}{{AB}}.\frac{{C{H^2}}}{{AC}} = \frac{{A{H^4}}}{{AB.AC}}\)(Vì AH2 = BH.CH)
Vậy BC.BE.CF = \(\frac{{AB.AC}}{{AH}}.\frac{{A{H^4}}}{{AB.AC}} = A{H^3}\).

