Cho tam giác ABC vuông tại A, đường cao AH. Gọi E, F lần lượt là chân các đường vuông góc hạ từ H xuống AB
Câu hỏi:
Cho tam giác ABC vuông tại A, đường cao AH. Gọi E, F lần lượt là chân các đường vuông góc hạ từ H xuống AB, AC và M là trung điểm của BC. Chứng minh rằng:
a) EF = AH.
b) AM ⊥ EF.
Trả lời:
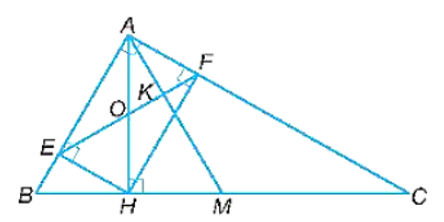
Tam giác OAE có OA = OE nên tam giác OAE cân tại O.
Suy ra ^OEA=^OAE
Mà AE song song với FH (do AFHE là hình chữ nhật) nên ^OHF=^OAE(hai góc so le trong).
Do đó, ^OHF=^OEA(2).
Lại có ^OHF+^OHE=^FHE=90°(3).
Từ (1), (2), (3) ta có:
Gọi K là giao điểm của AM và EF.
Khi đó,
Suy ra
Vậy AM vuông góc với EF tại K.
