Cho tam giác ABC vuông tại A. Về phía ngoài tam giác ABC, vẽ hai tam giác vuông cân ADB
Câu hỏi:
Cho tam giác ABC vuông tại A. Về phía ngoài tam giác ABC, vẽ hai tam giác vuông cân ADB (DA = DB) và ACE (EA = EC). Gọi M là trung điểm BC, I là giao điểm của DM với AB, K là giao điểm của EM với AC. Chứng minh:
a) Ba điểm D, A, E thẳng hàng.
b) Tứ giác IAKM là hình chữ nhật.
c) Tam giác DME là tam giác vuông cân.
Trả lời:
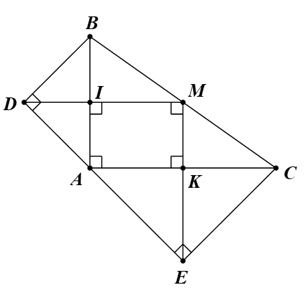
a) Ta có tam giác ADB vuông cân tại D.
Suy ra
Chứng minh tương tự, ta được
Ta có
Vậy ba điểm D, A, E thẳng hàng.
b) Tam giác ABC vuông tại A có AM là đường trung tuyến.
Suy ra MA = MB = MC.
Do đó M nằm trên đường trung trực của đoạn AB (1)
Chứng minh tương tự, ta được D nằm trên đường trung trực của đoạn AB (2)
Từ (1), (2), suy ra DM là đường trung trực của đoạn AB.
Mà DM cắt AB tại I.
Do đó DM ⊥ AB tại I.
Chứng minh tương tự, ta được ME ⊥ AC tại K.
Tứ giác IAKM, có:
Vậy tứ giác IAKM là hình chữ nhật.
c) Tam giác ADB vuông cân tại D có DI là đường cao.
Suy ra DI cũng là đường phân giác của tam giác ADB.
Do đó
Mà (do tứ giác IAKM là hình chữ nhật).
Vậy tam giác DME là tam giác vuông cân tại M.


