Cho tam giác ABC vuông tại A, đường cao AH, biết AH : AC = 3: 5 và AB = 15cm. a) Tính HB, HC. b) Gọi E, F lần lượt là hình chiếu của H trên AB và AC. Chứng minh AB.AC = EF.BC.
Câu hỏi:
Cho tam giác ABC vuông tại A, đường cao AH, biết AH : AC = 3: 5 và AB = 15cm.
a) Tính HB, HC.
b) Gọi E, F lần lượt là hình chiếu của H trên AB và AC. Chứng minh AB.AC = EF.BC.
Trả lời:
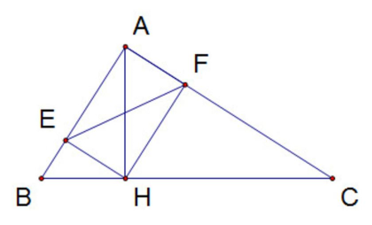
a) Xét △AHB và △CAB có:
chung
Do đó △AHB ∽ △CAB (g.g)
⇒
Ta lại có:
AB2 = HB.BC (hệ thức lượng)
⇒ BC = 152 : 9 = 25(cm)
⇒ HC = BC – HB = 25 – 9 = 16 cm
b) Xét tứ giác AEHF có:
Do đó AEHF là hình chữ nhật
⇒ EF = AH
Ta lại có: AB.AC = AH.BC = 2SABC nên AB.AC = EF.BC.


