Cho tam giác MNP vuông tại M, đường cao MH, có MN = 6cm, NP = 10cm. Tính MP, MH, NH.
Câu hỏi:
Trả lời:
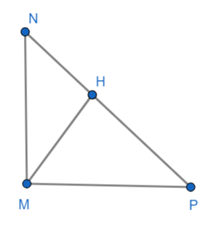
Áp dụng định lý Pytago:
Lại có: MH.NP = MN.MP
⇒
.Câu hỏi:
Trả lời:

Áp dụng định lý Pytago:
Lại có: MH.NP = MN.MP
⇒
.Câu 1:
Cho tam giác ABC có G là trọng tâm. Gọi H là chân đường cao hạ từ A sao cho . Điểm M di động nằm trên BC sao cho . Tìm x sao cho độ dài của đạt giá trị nhỏ nhất.
Câu 4:
Cho tam giác ABC có góc C nhọn, AH và BK là hai đường cao, HK = , diện tích tứ giác ABHK bằng 7 lần diện tích tam giác CHK. Khi đó bán kính đường tròn ngoại tiếp tam giác ABC bằng?
Câu 5:
Cho tam giác ABC nhọn. Gọi M, N, P lần lượt là trung điểm của AB, AC, BC. Kẻ đường cao AH. Chứng minh rằng tứ giác MNPH là hình thang cân.
Câu 7:
Cho tam giác vuông trong đó có một góc bằng trung bình cộng của hai góc còn lại, cạnh lớn nhất của tam giác đó bằng a. Diện tích của tam giác đó bằng bao nhiêu?
