Cho tam giác nhọn ABC có trực tâm H và góc BAC = 60 độ
Câu hỏi:
Cho tam giác nhọn ABC có trực tâm H và \(\widehat {BAC}\)= 60°. Gọi M, N, P theo thứ tự là chân các đường cao kẻ từ các đỉnh A, B, C của tam giác ABC và I là trung điểm của BC. Chứng minh rằng tam giác INP đều.
Trả lời:
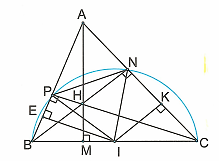
Ta thấy ΔBNC và ΔBPC là hai tam giác vuông có chung cạnh huyền BC nên bốn điểm B, P, N, C nằm trên đường tròn tâm I, đường kính BC.
Khi đó IN = IP ⇒ ΔINP cân tại I (1)
Tam giác ABN vuông tại N có: \(\widehat {ABN} + \widehat {BAN} = 90^\circ \)
⇒ \(\widehat {ABN} = 90^\circ - \widehat {BAN} = 90^\circ - 60^\circ = 30^\circ \)
Ta có \(\widehat {PBN}\) là góc nội tiếp và \(\widehat {PIN}\)là góc ở tâm cùng chắn cung
Do đó \(\widehat {PIN} = 2\widehat {PBN} = 60^\circ \) (2)
Từ (1) và (2) suy ra ΔINP đều.
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Xét xem dãy un = 3n – 1 có phải là cấp số nhân hay không? Nếu phải hãy xác định công bội.
Xem lời giải »
Câu 2:
Một vé xem phim có mức giá là 60000 đồng. Trong dịp khuyến mãi cuối năm 2018, số lượng người xem phim tăng lên 45% nên tổng doanh thu cũng tăng 8,75%. Hỏi rạp phim đã giảm giá mỗi vé bao nhiêu % so với giá bán ban đầu?
Xem lời giải »
Câu 3:
Tính giá trị của biểu thức: P = (x – 10)2 – x(x + 80) tại x = 0,87.
Xem lời giải »
Câu 4:
Tính giá trị biểu thức A = 100 – 99 + 98 – 97 + … + 4 – 3 + 2.
Xem lời giải »
Câu 5:
Cho 2 số tự nhiên y > x thỏa mãn (2y − 1)2 = (2y − x)(6y + x).
Chứng minh 2y – x là số chính phương.
Xem lời giải »
Câu 6:
Phân tích đa thức thành nhân tử: 9x2 – y2 + 4y – 4
Xem lời giải »
Câu 7:
Cho đường thẳng d: y = (m2 – 2)x + m – 1 với m là tham số. Tìm m để:
a) d song song với d1: y = 2x – 3.
b) d trùng với d': y = –x – 2.
Xem lời giải »
Câu 8:
a) Cho đoạn thẳng BC = 4cm. Vẽ tam giác đều ABC. Có thể vẽ được bao nhiêu tam giác như vậy?
b) Cho BC = 4cm. Vẽ hình vuông ABCD. Có thể vẽ được bao nhiêu hình vuông như vậy?
c) Vẽ hình chữ nhật có một cạnh dài 6cm; một cạnh dài 4 cm.
d) Vẽ hình thoi có cạnh bằng 3 cm và độ dài đường chéo bằng 6cm.
Xem lời giải »


