Cho tứ diện ABCD có các cạnh AB, AC, AD vuông góc với nhau từng đôi một và AB = 3cm
Câu hỏi:
Cho tứ diện ABCD có các cạnh AB, AC, AD vuông góc với nhau từng đôi một và AB = 3a , AC = 6a, AD = 4a. Gọi M, N, P lần lượt là trung điểm các cạnh BC, CD, DB. Tính thể tích khối đa diện AMNP.
A.
B.
C.
D.
Trả lời:
Chọn A
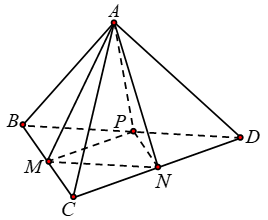
Cách 1: Khối tứ diện ABCD được chia thành bốn tứ diện có thể tích bằng nhau.
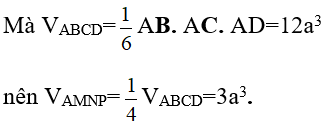
Cách 2:
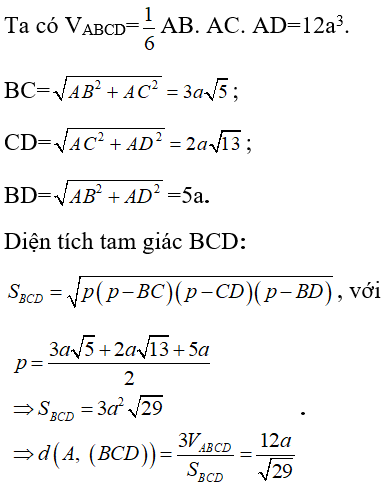
Mà M, N, P là trung điểm các cạnh BC, CD, BD nên hai tam giác BCD và MNP đồng dạng theo tỉ số
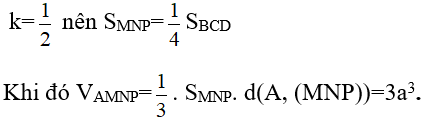
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Trong không gian Oxyz, cho đường thẳng và mặt phẳng (α): x + y -z – 2 = 0. Trong các đường thẳng sau, đường thẳng nào nằm trong mặt phẳng (α), đồng thời vuông góc và cắt đường thẳng d?
Xem lời giải »
Câu 2:
Trong không gian Oxyz, cho mặt phẳng (α): 2x + y -2z – 2 = 0, đường thẳng và điểm . Gọi Δ là đường thẳng nằm trong mặt phẳng (α), song song với d đồng thời cách d một khoảng bằng 3. Đường thẳng Δ cắt mặt phẳng (Oxy) tại điểm B. Độ dài đoạn thẳng AB bằng.
Xem lời giải »
Câu 3:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng (ABCD). Gọi G là trọng tâm của tam giác SAB và M, N lần lượt là trung điểm của SC, SD (tham khảo hình vẽ bên).
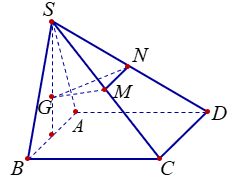
Tính côsin của góc giữa hai mặt phẳng (GMN) và (ABCD)
Xem lời giải »
Câu 4:
Trong không gian Oxyz, cho mặt phẳng x – z – 3 = 0 và điểm M (1; 1; 1). Gọi A là điểm thuộc tia Oz. Gọi B là hình chiếu của A lên (α). Biết rằng tam giác MAB cân tại M. Diện tích của tam giác MAB bằng:
Xem lời giải »


