Cho tứ diện ABCD và điểm M thuộc AB và N thuộc CD; điểm G nằm trong tam giác BCD. Tìm giao tuyến của (GMN) và (ACD).
Câu hỏi:
Cho tứ diện ABCD và điểm M thuộc AB và N thuộc CD; điểm G nằm trong tam giác BCD. Tìm giao tuyến của (GMN) và (ACD).
Trả lời:
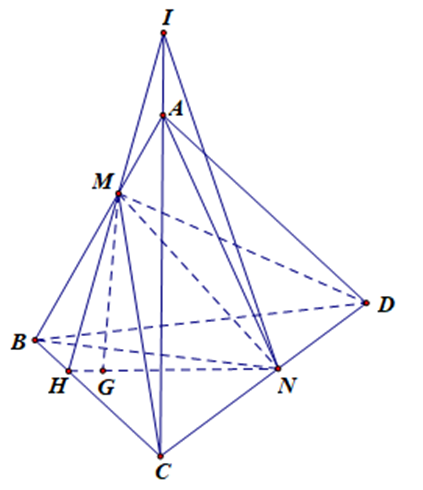
Có N ∈ CD ⊂ (ACD)
N ∈ (GMN)
Suy ra: N ∈ (ACD) ∩ (GMN) (1)
Trong mp(BCD) gọi H là giao điểm của NG và BC
Trong mp(ABC) gọi I là giao điểm AC và HM
Suy ra: I ∈ CA ⊂ (ACD)
I ∈ HM ⊂ (GMN)
Suy ra: I ∈ (ACD) ∩ (GMN) (2)
Từ (1) và (2) suy ra giao tuyến của (CAD) và (GMN) là NI.