Cho tam giác ABC. Gọi M là trung điểm BC và I là trung điểm AM. Chứng minh rằng 2ia ib ic =0
Câu hỏi:
Cho tam giác ABC. Gọi M là trung điểm BC và I là trung điểm AM. Chứng minh rằng
Trả lời:
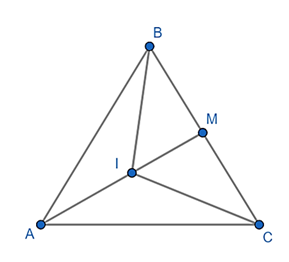
Vì I là trung điểm MA nên:
M là trung điểm của BC nên:
Vậy
Câu hỏi:
Cho tam giác ABC. Gọi M là trung điểm BC và I là trung điểm AM. Chứng minh rằng
Trả lời:

Vì I là trung điểm MA nên:
M là trung điểm của BC nên:
Vậy
Câu 1:
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M là trung điểm của SC.
a) Tìm giao điểm I của AM và (SBD).
b) Tìm giao điểm P của SD và (ABM). Chứng minh rằng P là trung điểm của SD.
c) Gọi N là điểm tùy ý trên cạnh AB. Tìm giao điểm K của MN và (SBD).
Câu 2:
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi K, J lần lượt là trọng tâm tam giác ABC và tam giác SBC. Xác định thiết diện hình chóp cắt bởi mặt phẳng chứa KI và song song AD.
Câu 3:
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và , SA = SB = SC, góc giữa đường thẳng SA và mặt phẳng (ABC) bằng 60 độ.Tính thể tích V của khối chóp S.ABCD.
Câu 4:
Câu 5:
Cho hình vuông ABCD có AB = 4, gọi E là trung điểm của cạnh CD và F là điểm thuộc cạnh AC sao cho CF= 3AF. Tính độ dài cạnh EF.
Câu 7:
