Cho x, y là các số thực dương thỏa mãn log9 x=log6 y= log4 (2x+y). Giá trị của x/y bằng
Câu hỏi:
Cho x, y là các số thực dương thỏa mãn . Giá trị của bằng
A. 2
B.
C.
D.
Trả lời:
Đáp án B
Giả sử . Suy ra:
.
Ta có :
Xem thêm bài tập Toán có lời giải hay khác:
Câu 3:
Với là các số thực dương tùy ý thỏa mãn , mệnh đề nào dưới đây đúng?
Xem lời giải »
Câu 8:
Cho a và b là hai số thực dương thỏa mãn . Giá trị của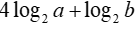 bằng
bằng
Xem lời giải »
