Điểm thuộc đồ thị hàm số trong đề thi Đại học có lời giải - Toán lớp 12

---

Điểm thuộc đồ thị hàm số trong đề thi Đại học có lời giải

Với Điểm thuộc đồ thị hàm số trong đề thi Đại học có lời giải Toán lớp 12 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Điểm thuộc đồ thị hàm số từ đó đạt điểm cao trong bài thi môn Toán lớp 12.

Dạng 1. Điểm đặc biệt thuộc đồ thị hàm số.

I. Phương pháp giải

1. Bài toán tìm điểm cố định của họ đường cong

Xét họ đường cong (Cm) có phương trình y = f(x; m). Hãy tìm những điểm cố định thuộc họ đường cong khi m thay đổi?

Phương pháp giải:

• Bước 1. Đưa phương trình y = f(x; m) về dạng sau: A.m + B = 0 hoặc Am² + Bm + C = 0

• Bước 2. Cho các hệ số bằng 0; ta thu được hệ phương trình và giải hệ phương trình:

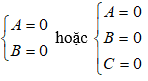
• Kết luận: Nếu hệ vô nghiệm thì đường cong không có điểm cố định. Nếu hệ có nghiệm thì điểm đó chính là điểm cố định của đường cong.

2. Bài toán tìm điểm thuộc đồ thị hàm số và có tọa độ nguyên

Cho đường cong (C) có phương trình y = f(x) (hàm phân thức). Hãy tìm những điểm có tọa độ nguyên của đường cong?

Phương pháp giải:

• Bước 1. Thực hiện phép chia đa thức; chia tử số cho mẫu số.

• Bước 2. Lập luận để tìm ra x.

Chú ý:

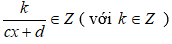
khi và chỉ khi (cx + d) ∈ Ư(k). Từ đó ta lập bảng.

3. Bài toán tìm điểm có tính chất đối xứng

Cho đường cong (C) có phương trình y = f(x). Tìm những điểm thuộc đường cong (C) và đối xứng với nhau qua một điểm; qua một đường thẳng.

Sử dụng tính chất hai điểm A, B đối xứng với nhau qua 1 điểm M (đường thẳng d). Khi đó; M là trung điểm AB(d là đường trung trực của AB).

4. Bài toán: Cho hàm số có đồ thị(C). Hãy tìm trên (C) hai điểm A và B thuộc hai nhánh của đồ thị hàm số sao cho khoảng cách AB ngắn nhất.

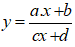
Phương pháp giải:

Đồ thị hàm số (C) có tiệm cận đứng là x = -d/c. Do tính chất hàm phân thức, đồ thị nằm về hai phía của tiệm cận đứng. Nên gọi hai số α, β là hai số dương

• Nếu A thuộc nhánh trái thì

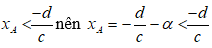
• Nếu B thuộc nhánh phải thì

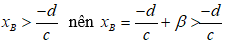
Sau đó:

tính

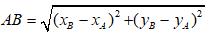
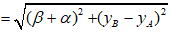
Sau đó áp dụng bất đẳng thức Cô-si ta sẽ ra kết quả.

5. Bài toán: Cho đồ thị hàm số (C) có phương trình y = f(x). Tìm tọa độ điểm M thuộc (C) để tổng khoảng cách từ M đến hai trục tọa độ nhỏ nhất (lớn nhất).

Phương pháp

• Gọi tọa độ M(x; y). Khi đó, tổng khoảng cách từ M đến hai trục tọa độ là: d = |x| + |y|

• Sử dụng phương pháp đánh giá, dùng bất đẳng thức hoặc xét chiều biến thiên của hàm số để xét tính d_max, d_min

6. Bài toán. Cho đồ thị hàm số ( C) có phương trình:

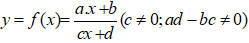
Tìm tọa độ điểm M trên (C) sao cho độ dài MI ngắn nhất (lớn nhất) - với I là điểm cho trước.

Phương pháp

• Gọi điểm

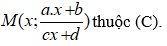
• Tính

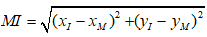
• Dùng bất đẳng thức, phương pháp tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số

II. Ví dụ minh họa

Ví dụ 1: Cho hàm số y = -x³ + 3x + 2. Tìm hai điểm trên đồ thị hàm số sao cho chúng đối xứng nhau qua điểm M(-1;3).

A. (-1; 0) và (-1; 6)      B.(-2; 0) và (0;6)

C. (0; 2) và (-2; 4)      D. Đáp án khác

Lời giải:

* Gọi A(x₀;y₀) và B là điểm đối xứng với A qua điểm M(-1; 3)

⇒ M là trung điểm của AB nên B(-2 - x₀; 6 - y₀).

* Do A và B thuộc đồ thị hàm số (C) nên:

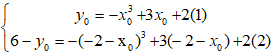
Từ (1) và (2) lấy vế cộng vế ta được:

6 = -x₀³ + 3x₀ + 2 - (-2 - x₀)³ + 3(-2 - x₀) + 2

⇔ 6 = -x₀³ + 3x₀ + 2 + 8 + 12x₀ + 6x₀² + x₀³ - 6 – 3x₀ + 2

⇔ 6x₀² + 12x₀ + 6 = 0

⇔ x₀ = -1 nên y₀ = 0

Vậy 2 điểm cần tìm là: (-1; 0) và (-1; 6).

Suy ra chọn đáp án A.

Ví dụ 2: Cho hàm số có đồ thị (C).

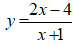
Tìm trên (C) hai điểm đối xứng nhau qua đường thẳng MN biết M(-3; 0) và N(-1; -1)

A. (0; -4) và (1; 3)      B. (2; 0) và (0; -4)

C. (1;3) và (2; 1)      D. (3; 1) và (2; -2)

Lời giải:

Ta có: MN→(2;-1)

* Phương trình đường thẳng MN:

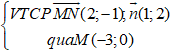
⇒ (MN): 1(x + 3) + 2(y - 0) = 0

hay x + 2y + 3 = 0 có hệ số góc k = -1/2.

* Phương trình đường thẳng d ⊥ MN có dạng: y = 2x + m.

Phương trình hoành độ giao điểm của (C) và (d):

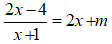
Nên 2x² + mx + m + 4 = 0 (1)

+ Để d cắt (C) tại hai điểm phân biệt A, B ⇔ Δ = m² - 8m - 32 > 0 (2)

Khi đó A(x₁; 2x₁ + m); B(x₂; 2x₂ + m) với x₁; x₂ là các nghiệm của (1)

Trung điểm của AB là

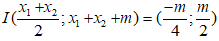
(theo định lý Vi-et)

Do A và B đối xứng nhau qua MN ⇔ I ∈ MN ⇔ m = -4

Suy ra (1)

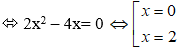
Nên A(0; -4); B(2; 0)

Suy ra chọn đáp án B.

Ví dụ 3: Cho hàm số y = x³ + mx² + 9x + 4. Xác định các giá trị của m để trên đồ thị hàm số có cặp điểm đối xứng nhau qua gốc tọa độ O.

A. m > 0      B. m < 0

C. m ≥ 0      D. m ≤ 0

Lời giải:

* Giả sử M(x₀; y₀); N(-x₀; -y₀) với x₀ ≠ 0 là cặp điểm đối xứng nhau qua O. Do M và N thuộc đồ thị hàm số nên ta có:

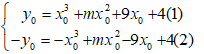
* Lấy (1) cộng với (2) vế với vế ta có: mx₀² + 4 = 0 (3)

Để (3) có nghiệm khi và chỉ khi m < 0 .

Vậy với m < 0 thì trên đồ thị hàm số có một cặp điểm đối xứng nhau qua gốc tọa độ O có hoành độ

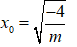
Suy ra chọn đáp án B.

Ví dụ 4: Tìm m để có hai điểm cực trị đối xứng với nhau qua đường thẳng d: 9x - 6y – 7 = 0

(Cm):

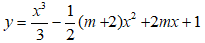
Lời giải:

Ta có: y' = x² – (m + 2).x + 2m

Và y' = 0 khi x = 2 hoặc x = m.

* Hàm số có hai điểm cực trị

⇔ Phương trình y' = 0 có hai nghiệm phân biệt ⇔ m ≠ 2

* Khi đó hai điểm cực trị của đồ thị hàm số đã cho là:

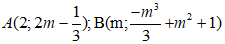
* Để A và B đối xứng với nhau qua đường thẳng (d) ⇔ AB ⊥ (d) và trung điểm I của đoạn AB thuộc (d).

Một vectơ chỉ phương của (d) là a−(2;3)

Mà

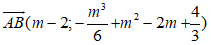
* AB vuông góc với (d) ⇔ AB−.n− = 0

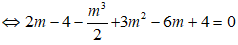
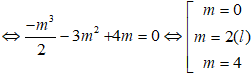
* Với m = 0 thì A(2;-1/3); B(0;1) suy ra trung điểm của AB là I(1; 1/3).

Thay tọa độ I vào phương trình của (d), ta được 0 = 0, suy ra I ∈ (d).

Vậy m = 0 thỏa mãn yêu cầu của bài toán.

* Với m = 4 thì A(2; 23/3); B(4; 19/3) suy ra I(3;7).

Thay tọa độ I vào phương trình (d) ta được 27 – 42 - 7 = 0 (sai) ⇒ I ∉ (d).

Vậy m = 4 không thỏa mãn yêu câu bài toán.

Vậy m = 0 thỏa mãn bài toán.

Ví dụ 5: Tìm trên đồ thị hàm số những điểm M sao cho khoảng cách từ M đến tiệm cận đứng bằng ba lần khoảng cách từ M đến tiệm cận ngang của đồ thị.

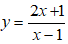
A. M(-4;7/5) hoặc M(2; 5).      B. M(4; 3) hoặc M(-2; 1).

C. M(4; 3) hoặc M(2;5).      D. M(-4;7/5) hoặc M(-2; 1) .

Lời giải:

Gọi à điểm thuộc đồ thị.

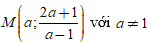
Đồ thị có đường tiệm cận đứng d: x = 1; đường tiệm cận ngang d': y = 2.

Theo yêu cầu bài toán ta có:

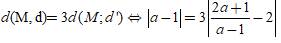
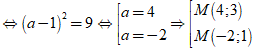
Suy ra chọn đáp án B.

Ví dụ 6: Cho hàm số y = x⁴ + mx² – m – 1 với m là tham số thực, có đồ thị là (C). Tìm tọa độ các điểm cố định thuộc đồ thị (C).

A. (-1; 0) và (1;0).      B. (1;0) và (0;1).

C. (-2;1) và (-2;3).      D. (2; 1) và (0;1) .

Lời giải:

Gọi điểm M(x₀; y₀) thuộc (C) .

Ta có: y₀ = x₀⁴ + mx₀² - m - 1 ⇔ (x₀² - 1)m + x₀⁴ - y₀ - 1 = 0 (1)

Để M là điểm cố định của (C) khi và chỉ khi (1) luôn đúng với mọi m

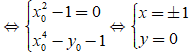
Suy ra chọn đáp án A.

Ví dụ 7: Cho hàm số có đồ thị là (C). Có bao nhiêu điểm thuộc đồ thị (C) mà tọa độ là số nguyên?

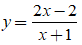
A. 2     B. 4

C. 5     D. 6

Lời giải:

Gọi M(x₀; y₀) ∈ (C)

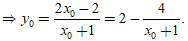
Để y₀ ∈ Z thì x₀ + 1 là ước của 4 hay x₀ + 1 ∈ {-1; 1; -2; 1; -4; 4}.

Suy ra x₀ ∈ {-5; -3; -2; 0; 1; 3}.

Vậy có 6 điểm thỏa mãn bài toán.

Suy ra chọn đáp án D.