Bài tập Tiếp tuyến của đồ thị hàm số trong đề thi Đại học có lời giải (2 dạng) - Toán lớp 12

---

Bài tập Tiếp tuyến của đồ thị hàm số trong đề thi Đại học có lời giải (2 dạng)

Với Bài tập Tiếp tuyến của đồ thị hàm số trong đề thi Đại học có lời giải (2 dạng) Toán lớp 12 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Tiếp tuyến của đồ thị hàm số từ đó đạt điểm cao trong bài thi môn Toán lớp 12.

Dạng 1: Viết phương trình tiếp tuyến của đồ thị hàm số.

I. Phương pháp giải

Cho hàm số y = f(x), gọi đồ thị của hàm số là (C).

Dạng 1. Viết phương trình tiếp tuyến của đồ thị hàm số (C): y = f(x) tại M(x₀; y₀)

♦ Phương pháp

• Bước 1. Tính y’= f’(x) suy ra hệ số góc của phương trình tiếp tuyến là k = y’(x₀)

• Bước 2. Phương trình tiếp tuyến của đồ thị (C) tại điểm M(x₀; y₀) có dạng

y - y₀ = f'(x₀).(x - x₀).

◊ Chú ý:

• Nếu đề bài yêu cầu viết phương trình tiếp tuyến tại điểm có hoành độ x₀ thì khi đó ta tìm y₀ bằng cách thế vào hàm số ban đầu, tức y₀ = f(x₀). Nếu đề cho y₀ ta thay vào hàm số để giải ra x₀.

• Nếu đề bài yêu cầu viết phương trình tiếp tuyến tại các giao điểm của đồ thị (C): y = f(x) và đường thẳng d: y= ax + b. Khi đó các hoành độ tiếp điểm là nghiệm của phương trình hoành độ giao điểm giữa d và (C)

Dạng 2. Viết phương trình tiếp tuyến của đồ thị hàm số (C): y = f(x) có hệ số góc k cho trước.

♦ Phương pháp

• Bước 1. Gọi M (x₀; y₀) là tiếp điểm và tính y' = f'(x).

• Bước 2. Hệ số góc tiếp tuyến là k' f'(x₀). Giải phương trình này tìm được x₀; thay vào hàm số được y₀

• Bước 3. Với mỗi tiếp điểm ta tìm được các tiếp tuyến tương ứng

d: y – y₀ = f'(x₀).(x - x₀)

◊ Chú ý: Đề bài thường cho hệ số góc tiếp tuyến dưới các dạng sau:

• Tiếp tuyến d // Δ: y = ax + b ⇒ hệ số góc của tiếp tuyến là k = a.

• Tiếp tuyến d ⊥ Δ: y = ax + b, (a ≠ 0) hệ số góc của tiếp tuyến là k = -1/a.

• Tiếp tuyến tạo với trục hoành một góc α thì hệ số góc của tiếp tuyến d là k = ±tanα

Dạng 3. Viết phương trình tiếp tuyến của đồ thị hàm số (C): y = f(x) biết tiếp tuyến đi qua điểm A(x_A; y_A).

♦ Phương pháp

Cách 1.

• Bước 1: Phương trình tiếp tuyến đi qua A(x_A; y_A) hệ số góc k có dạng

d: y = k(x - x_A) + y_A (*)

• Bước 2: d là tiếp tuyến của (C) khi và chỉ khi hệ sau có nghiệm:

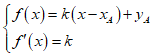
• Bước 3: Giải hệ này tìm được x suy ra k và thế vào phương trình (*), ta được tiếp tuyến cần tìm.

Cách 2.

• Bước 1. Gọi M(x₀; f(x₀)) là tiếp điểm và tính hệ số góc tiếp tuyến k = y'(x₀) = f'(x₀) theo x₀.

• Bước 2. Phương trình tiếp tuyến có dạng d: y = y'(x₀).(x – x₀) + y₀ (**). Do điểm A(x_A; y_A) d nên y_A = y'(x₀).(x_A- x₀) + y₀ giải phương trình này ta tìm được x₀.

• Bước 3. Thế x₀ vào (**) ta được tiếp tuyến cần tìm.

II. Ví dụ minh họa

Ví dụ 1: Cho hàm số y = -2x³ + 6x² - 5 có đồ thị (C). Viết phương trình tiếp tuyến của (C) tại điểm M thuộc (C) và có hoành độ bằng 3.

A. y = -18x + 49      B. y = -18x – 49

C. y = 18x + 49      D. y = 18x - 49

Lời giải:

Ta có: y' = -6x² + 12x.

Với x₀ = 3 thì y₀ = -5 ⇒ M(3; -5) và hệ số góc k = y'(3) = -18.

Vậy phương trình tiếp tuyến tại M là: y = -18(x - 3) – 5 = -18x + 49.

Suy ra chọn đáp án A.

Ví dụ 2: Cho hàm số y = x³ - 3x + 2 có đồ thị (C). Viết phương trình tiếp tuyến của (C) biết hệ số góc của tiêp tuyến đó bằng 9 :

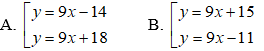
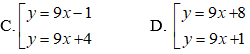
Lời giải:

Ta có đạo hàm y' = 3x² - 3.

Vậy k = y'(x₀) = 9

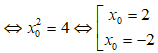
+ Với x₀ = 2 thì y₀ = 4 ta có tiếp điểm M(2; 4).

Phương trình tiếp tuyến tại M là: y = 9(x - 2) + 4 hay y = 9x - 14.

+ Với x₀ = -2 thì y₀ = 0 ta có tiếp điểm N(-2; 0).

Phương trình tiếp tuyến tại N là: y = 9(x + 2) + 0 hay y = 9x + 18.

Vậy có hai tiếp tuyến cần tìm là y = 9x - 14 và y = 9x + 18.

Suy ra chọn đáp án A.

Ví dụ 3: Cho hàm số y = -4x³ + 3x + 1 có đồ thị (C). Viết phương trình tiếp tuyến của (C) biết tiếp tuyến đi qua A(-1;2).

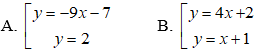
Lời giải:

Ta có y' = -12x² + 3.

+ Tiếp tuyến của (C) đi qua A(-1;2) với hệ số góc k có phương trình là: (d) y = k(x + 1) + 2

+ Do d là tiếp tuyến của (C) khi và chỉ khi hệ sau có nghiệm:

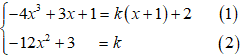
Thay k từ (2) vào (1) ta được :

⇔ -4x³ + 3x + 1 = (-12x² + 3).(x + 1) + 2

⇔ -4x³ + 3x + 1 = -12x³ - 12x² + 3x + 3 + 2

⇔ 8x³ + 12x² - 4 = 0

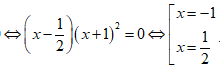
+ Với x = -1 thì k = -9. Phương trình tiếp tuyến là y = -9x - 7.

+ Với x = 1/2 ⇒ k = 0. Phương trình tiếp tuyến là y = 2.

Suy ra chọn đáp án A.

Ví dụ 4: Cho hàm số có đồ thị (C)

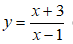
Viết phương trình tiếp tuyến của (C) biết tiếp tuyến đó vuông góc với đường thẳng d: y = x + 10 = 0 ?

Lời giải:

+ Điều kiện: x ≠ -1

+ Đạo hàm:

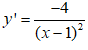
+ Do tiếp tuyến Δ cần tìm vuông góc với đường thẳng d: y = x + 10 = 0. Nên ta có: k_Δ.k_d = -1. Mà k_d = 1 nên k_Δ = -1

Suy ra:

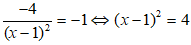
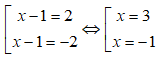
+ Với x = 3 thì y = 3. Phương trình tiếp tuyến tại điểm (3; 3) là:

y = -1(x - 3) + 3 hay y = -x + 6

+ Với x = -1 thì y = -1. Phương trình tiếp tuyến tại điểm (-1;-1) là:

y = -1(x + 1) - 1 hay y = -x - 2

Vậy có hai tiếp tuyến thỏa mãn là y = -x + 6 và y = -x - 2

Suy ra chọn đáp án B.

Dạng 2: Các bài toán về tiếp tuyến của đồ thị hàm số.

I. Phương pháp giải

Cho hàm số y = f(x) liên tục và có đạo hàm trên khoảng K. Để giải được các bài toán về tiếp tuyến của đồ thị hàm số ta cần chú ý:

+ Tính đạo hàm của hàm số.

+ Viết phương trình tiếp tuyến tại một điểm; đi qua một điểm; tiếp tuyến biết hệ số góc...

+ Hai đường thẳng song song có hệ số góc bằng nhau; hai đường thẳng vuông góc có tích hai hệ số góc bằng – 1.

+ Giao điểm của hai đồ thị hàm số.

+ Hệ thức Vi-et.

+ Khoảng cách từ một điểm đến một đường thẳng...

II. Ví dụ minh họa

Ví dụ 1: Cho hàm số y = -x⁴ – x² + 6 có đồ thị (C). Tiếp tuyến của đồ thị (C) cắt các trục Ox, Oy lần lượt tại hai điểm A, B sao cho OB = 36OA có phương trình là:

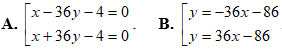
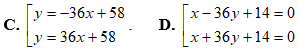
Lời giải:

Do OB = 36OA suy ra: OB/OA = 36 ⇒ y'(x₀) = ±36

• Với y'(x₀) = -36 nên -4x₀³ - 2x₀ = -36 ⇔ -4x₀³ - 2x₀ + 36 = 0 ⇔ x = 2

Vậy y₀ = y(2) = - 14.

Suy ra phương trình tiếp tuyến y= -36x + 58.

• Với y'(x₀) = 36

Nên x₀ = -2

Vậy y₀ = y(-2) = -14

Suy ra phương trình tiếp tuyến y = 36x + 58.

Suy ra chọn đáp án C.

Ví dụ 2: Cho hàm số có đồ thị là (C).

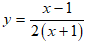
Gọi điểm M(x₀; y₀) với x₀ = -1 là điểm thuộc (C) biết tiếp tuyến của (C) tại điểm M cắt trục hoành, trục tung lần lượt tại hai điểm phân biệt A, B và tam giác OAB có trọng tâm G nằm trên đường thẳng d: 4x + y = 0. Hỏi giá trị của x₀ + 2y₀ bằng bao nhiêu?

A. -7/2      B. 7/2

C. 5/2      D. -5/2

Lời giải:

• Gọi

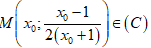
với x₀ ≠ -1 là điểm cần tìm.

• Gọi Δ tiếp tuyến của (C) tại M ta có phương trình.

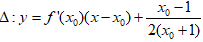
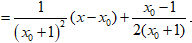
• Gọi A = Δ ∩ Ox

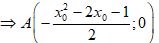
Và B = Δ ∩ Oy

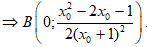
• Khi đó Δ tạo với hai trục tọa độ tam giác OAB có trọng tâm là:

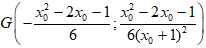
• Do G thuộc đường thẳng 4x + y = 0 nên

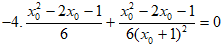
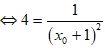
(vì A, B không trùng O nên x₀² - 2x₀ - 1 ≠ 0)

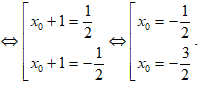
• Vì x₀ > -1 nên chỉ chọn x₀ = -1/2

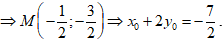
Suy ra chọn đáp án A.

Ví dụ 3: Cho hàm số y = x⁴ - 2mx² + m (1), m là tham số thực. Kí hiệu (Cm) là đồ thị hàm số đã cho; gọi d là tiếp tuyến của (Cm) tại điểm có hoành độ bằng 1. Tìm m để khoảng cách từ điểm B(3/4; 1) đến đường thẳng d đạt giá trị lớn nhất?

A. m = -1      B. m = 1

C. m = 2      D. m = -2

Lời giải:

+ Gọi A là điểm thuộc đồ thị hàm số có hoành độ bằng 1 nên A(1; 1 - m).

Ngoài ra y' = 4x³ – 4mx

Suy ra: y'(1) = 4 - 4m

+ Phương trình tiếp tuyến của (Cm) tại A là :

y - 1 + m = y'(1).(x - 1) hay (4 - 4m)x - y – 3(1 - m) = 0

+ Khi đó

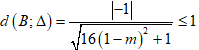
Dấu ‘=’ xảy ra khi m = 1.

+ Do đó d(B; Δ) lớn nhất bằng 1 khi và chỉ khi m = 1.

Suy ra chọn đáp án B.

Ví dụ 4: Cho hàm số có đồ thị là (C).

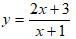
Có bao nhiêu tiếp tuyến của đồ thị (C) tại những điểm thuộc đồ thị có khoảng cách đến đường thẳng d₁: 3x + 4y – 2 = 0 bằng 2.

A. 2.     B. 3.

C. 4.     D. 0.

Lời giải:

• Giả sử M(x₀; y₀) ∈ (C)

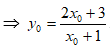
• Ta có:

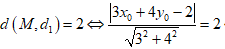
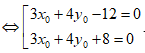
• Với 3x₀ + 4y₀ - 12 = 0

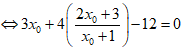
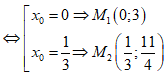
• Với 3x₀ + 4y₀ + 8 = 0

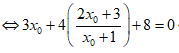
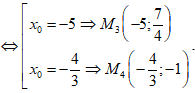
Ứng với 4 điểm M tìm được ta viết được 4 tiếp tuyến thỏa mãn đầu bài.

Suy ra chọn đáp án C.

Ví dụ 5: Cho hàm số có đồ thị là (C).

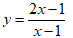
Gọi I là giao điểm hai tiệm cận của (C). Tìm điểm M thuộc (C) có hoành độ lớn hơn 1 sao cho tiếp tuyến của (C) tại M vuông góc với đường thẳng MI?

A. M(4; 7/3)     B. M(3; 5/2)

C. M(2; 3)      D. M(5; 3)

Lời giải:

• Đồ thị hàm số có tiệm cận đứng là x = 1 và tiệm cận ngang là y = 2. Giao điểm của hai tiệm cận là I(1; 2).

• Gọi

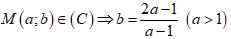
• Phương trình tiếp tuyến của (C) tại M là:

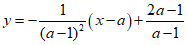
• Phương trình đường thẳng MI là:

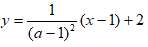
• Tiếp tuyến tại M vuông góc với MI nên ta có

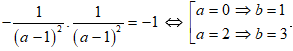
Vì yêu cầu hoành độ lớn hơn 1 nên điểm cần tìm là M(2;3) .

Suy ra chọn đáp án C.

Ví dụ 6: Cho hàm số có đồ thị là (C)

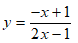
Đường thẳng d: y = x + m. Với mọi m ta luôn có d cắt (C) tại 2 điểm phân biệt A, B. Gọi k₁, k₂ lần lượt là hệ số góc của các tiếp tuyến với (C) tại A, B. Tìm m để tổng k₁ + k₂ đạt giá trị lớn nhất.

A. m = -1      B. m = -2

C. m = 3      D. m = -5

Lời giải:

• Phương trình hoành độ giao điểm của d và (C) là

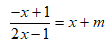
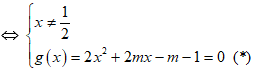
• Theo định lí Viet ta có x₁ + x₂ = -m; x₁.x₂ = (-m - 1)/2. Giả sử A(x₁; y₁); B(x₂; y₂).

• Ta có

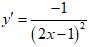
Nên tiếp tuyến của (C) tại A và B có hệ số góc lần lượt là:

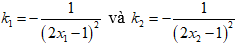
Vậy

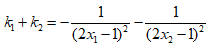
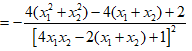
• Dấu "=" xảy ra ⇔ m = -1.

Vậy k₁ + k₂ đạt giá trị lớn nhất bằng - 2 khi m = -1.

Suy ra chọn đáp án A.