Giả sử AB là một dây cung của đường tròn (O). Trên cung nhỏ AB lấy các điểm C và D sao
Câu hỏi:
Giả sử AB là một dây cung của đường tròn (O). Trên cung nhỏ AB lấy các điểm C và D sao cho . Chứng minh AB và CD song song.
Trả lời:
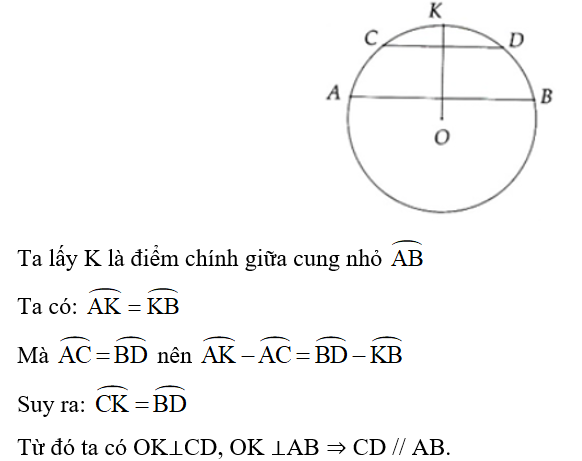
Câu hỏi:
Giả sử AB là một dây cung của đường tròn (O). Trên cung nhỏ AB lấy các điểm C và D sao cho . Chứng minh AB và CD song song.
Trả lời:

Câu 2:
Cho x,y,z là các số nguyên thỏa mãn: (x - y)(y - z)(z – x) = x + y + z. Chứng minh x + y + z chia hết cho 27.
Câu 6:
Cho hình bình hành ABCD. Trên các cạnh AB và CD lần lượt lấy các điểm M và N sao cho AM = DN. Đường trung trực của BM lần lượt cắt các đường thẳng MN và BC tại E và F.
a) Chứng minh E và F đối xứng với nhau qua AB.
b) Chứng minh tứ giác MEBF là hình thoi.
c) Hình bình hành ABCD có thêm điều kiện gì để tứ giác BCNE là hình thang cân.
Câu 8:
Cho hình bình hành ABCD có . Tia phân giác của qua trung điểm I của AB. Kẻ AH vuông góc với DC. Chứng minh rằng:
a) AB = 2AD.
b) DI = 2AH.
c) AC vuông góc với AD.
