Giá trị lớn nhất và giá trị nhỏ nhất của hàm số y=2^sin^2x+2^cos^2x là

Câu hỏi:

Giá trị lớn nhất và giá trị nhỏ nhất của hàm số $y = 2^{\sin^{2} x} + 2^{\cos^{2} x}$ là:

A. $\underset{ℝ}{m i n} y = 2 \sqrt{2}; \underset{ℝ}{m a x} y = 3$

B. $\underset{ℝ}{m i n} y = 2; \underset{ℝ}{m a x} y = 3$

C. $\underset{ℝ}{m i n} y = 3; \underset{ℝ}{m a x} y = 3 \sqrt{2}$

D. $\underset{ℝ}{m i n} y = 2; \underset{ℝ}{m a x} y = 3 \sqrt{2}$

Trả lời:

Chọn A.

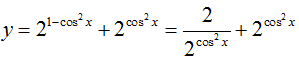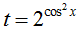Ta có: . Đặt , do 0 ≤ cos²x ≤ 1 nên ta có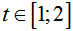

Xét hàm s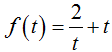ố có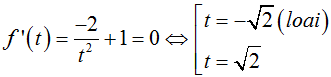

Lại có

Vậy

Câu 1:

Cho hàm số y = log₂( 4^x- 2^x+ m) có tập xác định D = R khi:

Câu 2:

$y = \log_{2} (\frac{4^{x} + 2^{x + 1} + 10}{2^{x} + 1} - m)$ có tập xác định D = R khi đó có bao nhiêu giá trị nguyên dương của tham số m ?

Câu 3:

Cho hàm số $y = \sqrt[3]{\ln^{2} (x^{2} + 1) + 2}$ . Mệnh đề nào dưới đây là đúng?

Câu 4:

Cho x; y là các số thực dương thỏa $\log_{9} x = \log_{6} y = \log_{4} (\frac{x + y}{6})$ . Tính tỉ số x/y

Câu 5:

Giá trị lớn nhất và nhỏ nhất của hàm số y = 4^x- 2^x+1 trên đoạn [- 1;1]

Câu 6:

Giá trị lớn nhất và nhỏ nhất của hàm số $y = 5^{\sqrt{x}} + 5^{1 - \sqrt{x}}$ trên đoạn [0;1] là:

Các dạng bài tập Toán lớp 12