Lý thuyết tổng hợp chương Mặt nón, mặt trụ, mặt cầu - Toán lớp 12

Lý thuyết tổng hợp chương Mặt nón, mặt trụ, mặt cầu

Tài liệu Lý thuyết tổng hợp chương Mặt nón, mặt trụ, mặt cầu Toán lớp 12 sẽ tóm tắt kiến thức trọng tâm về chương Mặt nón, mặt trụ, mặt cầu từ đó giúp học sinh ôn tập để nắm vứng kiến thức môn Toán lớp 12.

A. Tóm tắt lý thuyết

** MẶT NÓN

    Cho hình nón có chiều cao là h, bán kính đáy r và đường sinh là l thì có:

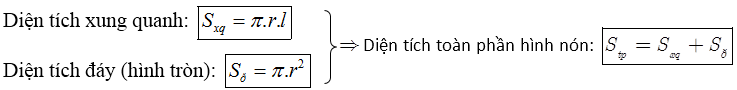
    - Thể tích khối nón: .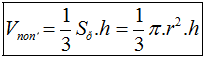

** MẶT TRỤ

    Cho hình trụ có chiều cao là và bán kính đáy bằng r, khi đó:

    - Diện tích xung quanh của hình trụ: S_xq = 2πrh

    - Diện tích toàn phần của hình trụ: S_tp = S_xq + 2.S_Đay = 2πrh + 2πr²

    - Thể tích khối trụ: V = B.h = πr²h

** MẶT CẦU

    • Diện tích mặt cầu: S_C = 4πR².

    • Thể tích mặt cầu: V_C = (4/3)πR³.

** KỸ THUẬT XÁC ĐỊNH MẶT CẦU NGOẠI TIẾP HÌNH CHÓP.

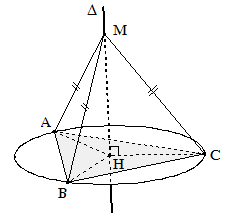
    Bước 1: Xác định tâm của đường tròn ngoại tiếp đa giác đáy. Dựng Δ: trục đường tròn ngoại tiếp đa giác đáy.

    Bước 2: Lập mặt phẳng trung trực (α) của một cạnh bên.

    Lúc đó : - Tâm O của mặt cầu: Δ ∩ mp(α) = {O}

    - Bán kính: R = SA (= SO) . Tuỳ vào từng trường hợp.

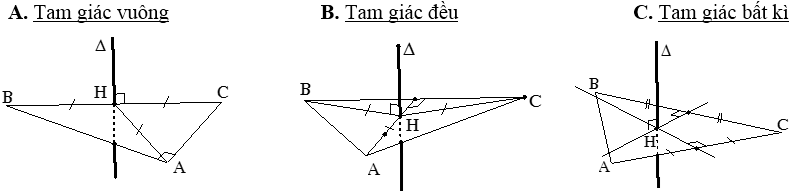
    Lưu ý: Kỹ năng xác định trục đường tròn ngoại tiếp đa giác đáy.

    1. Trục đường tròn ngoại tiếp đa giác đáy: là đường thẳng đi qua tâm đường tròn ngoại tiếp đáy và vuông góc với mặt phẳng đáy.

    Tính chất: ∀M ∈ Δ: MA = MB = MC

    Suy ra: MA = MB = MC ⇔ M ∈ Δ

    2. Các bước xác định trục:

    - Bước 1: Xác định tâm H của đường tròn ngoại tiếp đa giác đáy.

    - Bước 2: Qua H dựng Δ vuông góc với mặt phẳng đáy.

    VD: Một số trường hợp đặc biệt

    3. Lưu ý: Kỹ năng tam giác đồng dạng

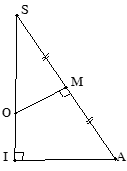
    ΔSMO đồng dạng với ΔSIA .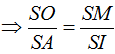

    4. Nhận xét quan trọng:

    ⇒ SM là trục đường tròn ngoại tiếp ΔABC.