Tìm nguyên hàm: I=∫sinx.ln(cosx)dx
Câu hỏi:
Tìm nguyên hàm:
A. –cosxln(cosx)-cosx+C
B. cosx. lnsinx +sinx +C
C.-sinx.ln(cosx)-cosx+C
D. sinx.ln(sinx)-sinx+C
Trả lời:
Chọn A.
Đặt
ta chọn
Suy ra
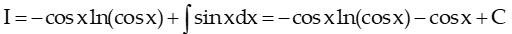
Xem thêm bài tập Toán có lời giải hay khác:
Câu 3:
Họ nguyên hàm của hàm số là hàm số nào?
Xem lời giải »
Câu 4:
Giá trị m để hàm số là một nguyên hàm của hàm số
Xem lời giải »
Câu 6:
Cho .Tìm m để nguyên hàm của hàm số f(x) thỏa mãn F(0)=1 và
Xem lời giải »
