Tính mô-đun của số phức z, biết z^3 + 12i = z ngang
Câu hỏi:
Tính mô-đun của số phức z, biết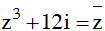 
và z có phần thực dương.
A. 2
B. 1
C.3
D.
Trả lời:
Chọn D.
Giả sử z = x + yi (x, y R); từ giả thiết :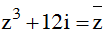 
Nên ( x + yi) 3+ 12i = x - yi
Hay x3 - 3xy2+ ( 3x2y - y3 +12) i = x - yi
Ta có hệ phương trình là x3 - 3xy2 = x (1) và 3x2y - y3 + 12 = - y ( 2)
Do x > 0 nên từ (1) x2 = 3y2+ 1. Thế vào (2) ta được:
3( 3y2 + 1) y - y3 + 12 = -y
Hay 2y3+ y + 3 = 0 (3)
Giải phương trình (3) ta được y = -1; x2 = 4. Do x > 0 nên x = 2.
Vậy z = 2 - i và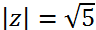 
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Trên mặt phẳng tọa độ Oxy, tìm tập hợp các điểm biểu diễn các số phức z thỏa mãn điều kiện |z – 2| + |z + 2| = 10.
Xem lời giải »
Câu 2:
Cho số phức z thỏa mãn |z + 2| + |z – 2| = 8. Trong mặt phẳng phức tập hợp những điểm M biểu diễn cho số phức z là?
Xem lời giải »
Câu 4:
Tìm nghiệm của phương trình: ( z + 3 - i)2 - 6( z + 3 - i) + 13 = 0
Xem lời giải »
Câu 5:
Giải phương trình sau: ( z2 + z) 2 + 4( z2+ z) - 12 = 0
Xem lời giải »
Câu 6:
Giải phương trình sau: ( z2 + 3z + 6) 2 + 2z( z2 + 3z + 6) - 3z2 = 0
Xem lời giải »
Câu 7:
Cho phương trình: ( z2 - z) ( z + 3) (z + 2) = 10 .Tính tổng tất cả các phần thực của các nghiệm phương trình trên.
Xem lời giải »
Câu 8:
Cho A; B; C tương ứng là các điểm trong mặt phẳng phức biểu diễn các số phức z1 = 1 + 2i; z2 = -2 + 5i ; z3 = 2 + 4i . Số phức z biểu diễn bởi điểm D sao cho tứ giác ABCD là hình bình hành là
Xem lời giải »
