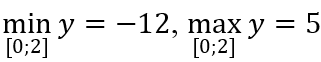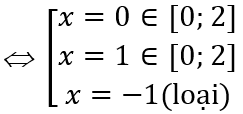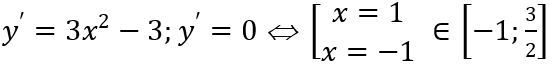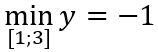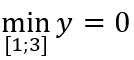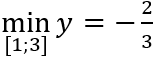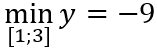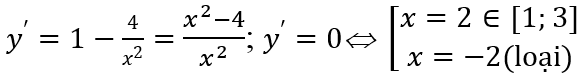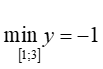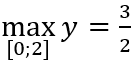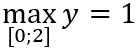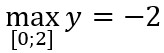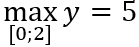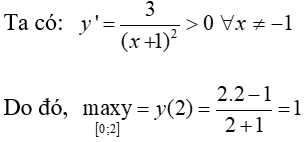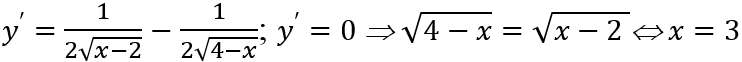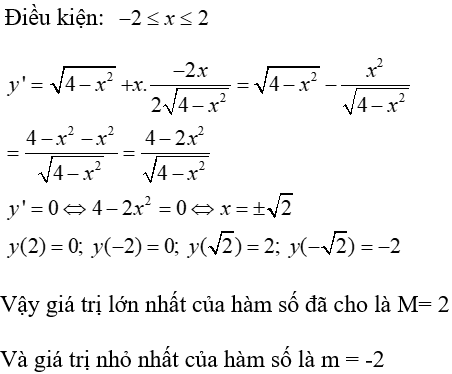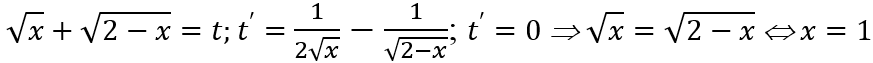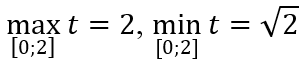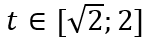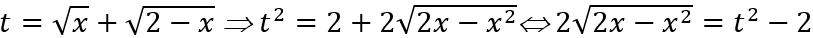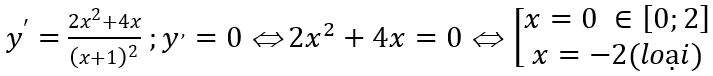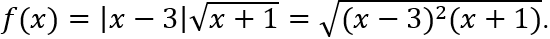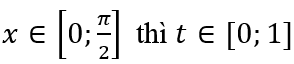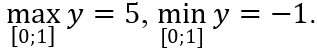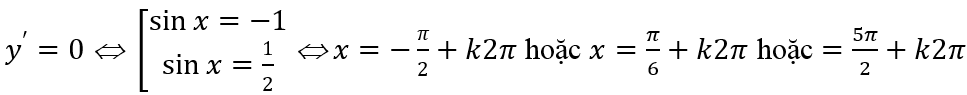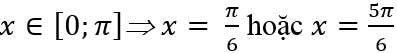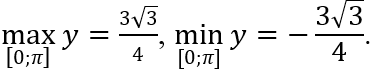Bài tập trắc nghiệm tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số cực hay - Toán lớp 12

---

Bài tập trắc nghiệm tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số cực hay

Với Bài tập trắc nghiệm tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số cực hay Toán lớp 12 tổng hợp 15 bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số từ đó đạt điểm cao trong bài thi môn Toán lớp 12.

Câu 1: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = -2x⁴ + 4x² + 5 trên đoạn [0; 2] là:

A.

B.

C. 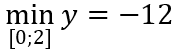và không có giá trị lớn nhất

D. 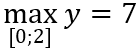và không có giá trị nhỏ nhất

Lời giải:

Đáp án : B

Giải thích :

Ta có y' = -8x³ + 8x ; y' = 0

Vì y(0) = 5; y(1) = 7; y(2) = -11 nên

Câu 2: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = x³ - 3x + 3 trên [-1; 3/2] lần lượt là;

A. 15/8 và 5

B. 5 và 1

C. 1 và 15/8

D. 5 và 15/8

Lời giải:

Đáp án : B

Giải thích :

Ta có

Vì y(-1) = 5; y(1) = 1; y(3/2) = 15/8 nên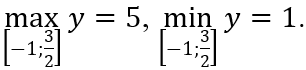

Câu 3: Giá trị nhỏ nhất của hàm số y = x - 5 + 4/x trên đoạn [1; 3] là:

A.

B.

C.

D.

Lời giải:

Đáp án : A

Giải thích :

ĐKXĐ: x ≠ 0;

Có y(1) = 0; y(2) = -1; y(3) = -2/3 nên

Câu 4: Giá trị lớn nhất của hàm số 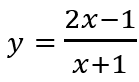trên đoạn [0;2] là:

A.

B.

C.

D.

Lời giải:

Đáp án : B

Giải thích :

Câu 5: Giá trị nhỏ nhất của hàm số 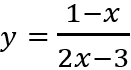trên [0;2] là:

A. 0

B. -1/3

C. -1

D. 2

Lời giải:

Đáp án : B

Giải thích :

Ta có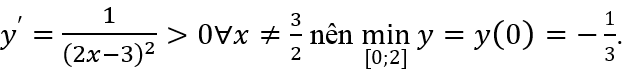

Câu 6: Giá trị lớn nhất của hàm số 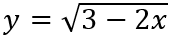trên đoạn [-1; 1] là;

A. √5

B. 3

C. 1

D. √3

Lời giải:

Đáp án : A

Giải thích :

Ta có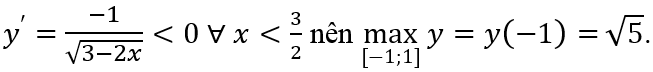

Câu 7: Giá trị lớn nhất M của hàm số 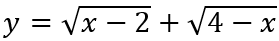là:

A. M = 1

B. M = 2

C. M = 3

D. M = 4

Lời giải:

Đáp án : B

Giải thích :

ĐKXĐ: 2 ≤ x ≤ 4

Ta có

Vì y(2) = y(4) = √2; y(3) = 2 nên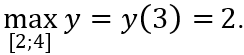

Câu 8: Giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số 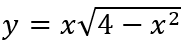là

A. M = 2; m = 0

B. M = √2; m = -√2

C. M = 2; m = -2

D. M = √2; m = 0

Lời giải:

Đáp án : C

Giải thích :

Câu 9:Giá trị lớn nhất M của hàm số 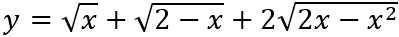là:

A. M = √2

B. M = 4

C. M = √2

D. M = 8

Lời giải:

Đáp án : B

Giải thích :

TXĐ D = [0; 2]

Đặt

Vì y(0) = y(2) = √2; y(1) = 2 nên

Khi đó

Vì

Khi đó hàm số trở thành y = t² + t - 2; y' = 2t + 1 > 0 ∀ x ∈[√2;2]

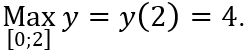
Câu 10: (Đề thi Đại học Khối D – 2011). Cho hàm số 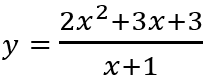giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số trên đoạn [0; 2] là:

A. M = 17/3; m = 3     C. M = 17/3; m = -5

B. M = 3; m = -5     D. M = -3; m = 5

Lời giải:

Đáp án : A

Giải thích :

Hàm số xác định, liên tục trên đoạn [0; 2]

Ta có

Vì y(0) = 3; y(2) = 17/3. Vậy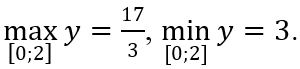

Câu 11: Gọi M, N lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số 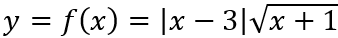trên đoạn [0; 4]. Tình biểu thức M + 2N

A. (16√3)/9

B. 3 + √5

C. (16√3)/3

D. √5

Lời giải:

Đáp án : A

Giải thích :

Xét hàm số g(x) = (x - 3)²(x + 1), x ∈ [0; 4].

g'(x) = 2(x - 3)(x + 1) + (x - 3)² = (x - 3)(2(x + 1) + x - 3) = (x - 3)(3x - 1).

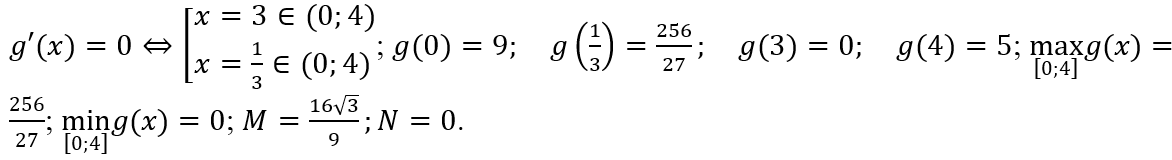
Vậy M + 2N = (16√3)/9.

Câu 12: Hàm số y = √3sin⁡x + cos⁡x có giá trị lớn nhất và giá trị nhỏ nhất là:

A. 0 và -1

B. √3 và 0

C. √3 và -1

D. 2 và -2

Lời giải:

Đáp án : D

Giải thích :

Ta có √3sin⁡x + cos⁡x = 2(√3/2 sin⁡ x + 1/2 cos⁡x ) = 2sin⁡(x + π/6)

Vì -1 ≤ sin⁡(x + π/6) ≤ 1 nên -2 ≤ 2sin⁡(x + π/6) ≤ 2 .

Câu 13: Giá trị nhỏ nhất m của hàm số y = 2cos³⁡x - 9/2 cos²⁡x + 3cos⁡x + 1/2 là:

A. m = -24

B. m = -12

C. m = -9

D. m = 1

Lời giải:

Đáp án : C

Giải thích :

Đặt cos⁡x = t (-1 ≤ t ≤ 1)

Hàm số trở thành 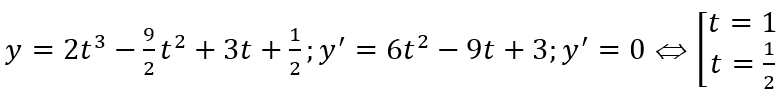(thỏa mãn)

Ta có y(-1) = -9; y(1)= 1 ; y(1/2) = 9/8 nên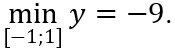

Câu 14:Hàm số y = cos⁡2x - 4sin⁡x + 4 có giá trị lớn nhất, giá trị nhỏ nhất trên đoạn [0; π/2] là

A. π/2 và 0

B. 5 và 1

C. 5 và -1

D. 9 và 1

Lời giải:

Đáp án : C

Giải thích :

Ta có y = cos⁡2x - 4sin⁡x + 4 = -2sin²⁡x - 4sin⁡x + 5

Đặt sin⁡x = t khi

Hàm số trở thành y = -2t² - 4t + 5; y' = -4t - 4; y' = 0 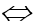t = -1 (loại)

Ta có y(0) = 5; y(1) = -1 nên

Câu 15: Hàm số y = cos⁡x(sin⁡x+1) có giá trị lớn nhất và giá trị nhỏ nhất trên đoạn [0; π] là:

A. 1 và -1     B. 2 và -2     C. (3√3)/4 và -(3√3)/4     D. 2 và 0

Lời giải:

Đáp án : C

Giải thích :

TXĐ: D = R

Ta có y' = -sin⁡x(sin⁡x + 1) + cos²⁡x = -2sin²⁡x - sin⁡ x + 1

Vì

Khi đó y(0) = 1; y(π/6) = (3√3)/4; y(5π/6) = -(3√3)/4; y(π) = -1

Vậy