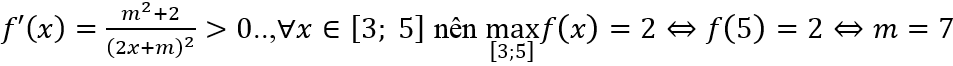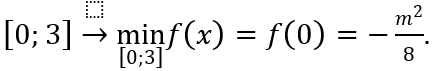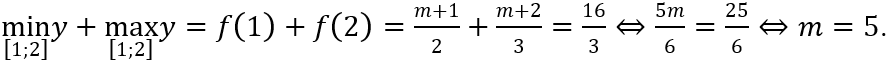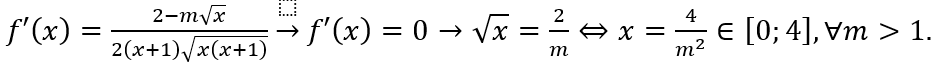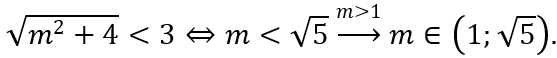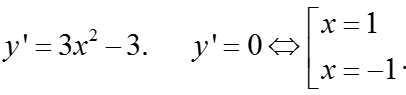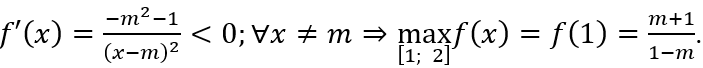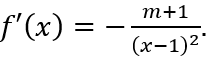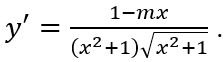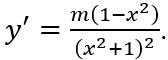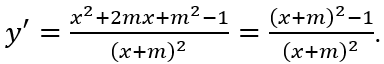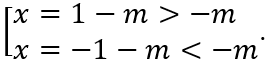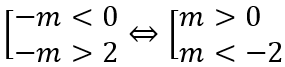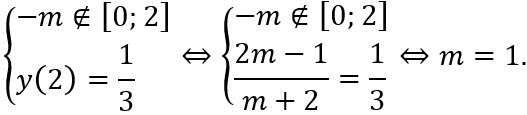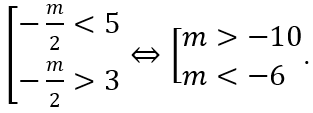Trắc nghiệm Tìm m để hàm số có Giá trị lớn nhất, Giá trị nhỏ nhất thoả mãn điều kiện - Toán lớp 12

---

Trắc nghiệm Tìm m để hàm số có Giá trị lớn nhất, Giá trị nhỏ nhất thoả mãn điều kiện

Với Trắc nghiệm Tìm m để hàm số có Giá trị lớn nhất, Giá trị nhỏ nhất thoả mãn điều kiện Toán lớp 12 tổng hợp 12 bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Tìm m để hàm số có Giá trị lớn nhất, Giá trị nhỏ nhất thoả mãn điều kiện từ đó đạt điểm cao trong bài thi môn Toán lớp 12.

Câu 1: Cho hàm số f(x) = x³ + (m² + 1)x + m² - 2 với m là tham số thực. Tìm tất cả các giá trị của m để hàm số có giá trị nhỏ nhất trên đoạn [0; 2] bằng 7.

A. m = ±1.    B. m = ±√7.    C. m = ±√2.    D. m = ±3.

Lời giải:

Đáp án : D

Giải thích :

Đạo hàm f'(x) = 3x² + m² + 1 > 0,∀ x ∈ R.

Suy ra hàm số f(x) đồng biến trên [0; 2] →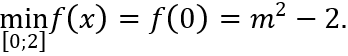

Theo bài ra: 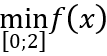f(x) = 7 ⇔ m² - 2 = 7 ⇔ m = ±3.

Câu 2: Cho hàm số 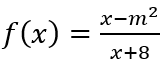với m là tham số thực. Tìm giá trị lớn nhất của m để hàm số có giá trị nhỏ nhất trên đoạn [0; 3] bằng -2.

A. m = 4.    B. m = 5.    C. m = -4.    D. m = 1.

Lời giải:

Đáp án : A

Giải thích :

Đạo hàm 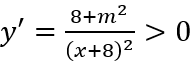,∀ x ∈ [0; 3].

Suy ra hàm số f(x) đồng biến trên đoạn

Theo bài ra: 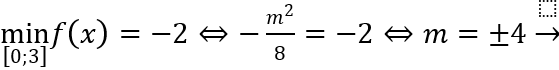giá trị m lớn nhất là m = 4.

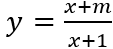
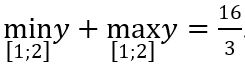
Câu 3: Cho hàm số . Với tham số m bằng bao nhiêu thì thỏa mãn .

A. m = 0.    B. m = 2.    C. m = 4.    D. m = 5.

Lời giải:

Đáp án : D

Giải thích :

Đạo hàm .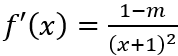

Suy ra hàm số f(x) là hàm số đơn điệu trên đoạn [1; 2] với mọi m ≠ 1.

Khi đó

Câu 4: Cho hàm số 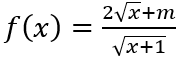với m là tham số thực. Tìm tất cả các giá trị của m > 1 để hàm số có giá trị lớn nhất trên đoạn [0; 4] nhỏ hơn 3.

A. m ∈ (1; 3).    B. m ∈ (1; 3√5 - 4).    C. m ∈ (1; √5).    D. m ∈ (1; 3].

Lời giải:

Đáp án : C

Giải thích :

Đạo hàm

Lập bảng biến thiên, ta kết luận được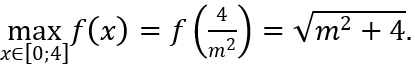

Vậy ta cần có

Câu 5: Cho hàm số y = x³ - 3x + 1 . Tìm tìm tập hợp tất cả giá trị m > 0, để giá trị nhỏ nhất của hàm số trên D = [m + 1; m + 2] luôn bé hơn 3 là:

A. (0; 1).    B. (1/2; 1)     C. (-∞; 1)\{-2}     D. (0; 2).

Lời giải:

Đáp án : A

Giải thích :

Ta có :

Hàm số đồng biến trên khoảng (1; +∞).

Trên D =[m + 1; m + 2], với m > 0 , ta có :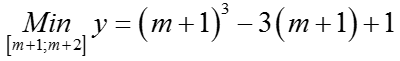

Ycbt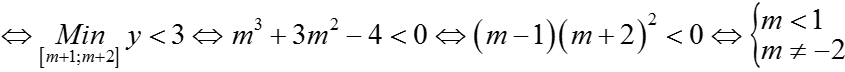

Kết hợp điều kiện Suy ra m 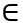(0; 1)

Câu 6: Tìm tất cả các giá trị của m để hàm số 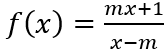có giá trị lớn nhất trên [1; 2] bằng -2.

A. m = -3.    B. m = 2.    C. m = 4.    D. m = 3.

Lời giải:

Đáp án : D

Giải thích :

Tập xác định: D = R\{m} ⇒ m ∉ [1; 2].

Theo đề bài 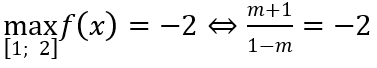⇔ m + 1 = 2m - 2 ⇔ m = 3.

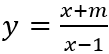
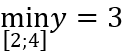
Câu 7: Cho hàm số , với tham số m bằng bao nhiêu thì .

A. m = 1.    B. m = 3.    C. m = 5.    m = -1.

Lời giải:

Đáp án : C

Giải thích :

Đạo hàm

TH1. Với m > - 1 suy ra f'(x) = -(m + 1)/(x - 1)² < 0; ∀ x ≠ 1 nên hàm số f(x) nghịch biến trên mỗi khoảng xác định. Khi đó 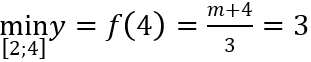⇔ m = 5 (chọn).

TH2. Với m < - 1 suy ra f'(x) = -(m + 1)/(x - 1)² > 0; ∀ x ≠ 1 nên hàm số f(x) đồng biến trên mỗi khoảng xác định. Khi đó 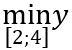y = f(2) = m + 2 = 3 ⇔ m = 1 (loại).

Câu 8: Cho hàm số 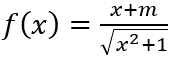. Tìm tất cả các giá trị của tham số thực m để hàm số đạt giá trị lớn nhất tại điểm x = 1.

A. m = 2.    B. m = 1.    C. Không có giá trị m.     D. m = -3.

Lời giải:

Đáp án : B

Giải thích :

Tập xác định D = R ,

Vì hàm số liên tục và có đạo hàm trên R nên để hàm số đạt GTLN tại x = 1, điều kiện cần là y'(1) = 0 ⇔ 1 - m = 0 ⇔ m = 1.

Khi đó ta lập bảng biến thiên và hàm số đạt GTLN tại x = 1.

Câu 9: Tìm tất cả các giá trị thực khác 0 của tham số m để hàm số 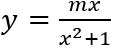đạt giá trị lớn nhất tại x = 1 trên đoạn [-2; 2]?

A. m = -2.    B. m < 0.    C. m > 0.    D. m = 2.

Lời giải:

Đáp án : C

Giải thích :

Ta có

m ≠ 0. Khi đó: y' = 0 ⇔ .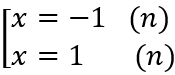

Vì hàm số đã cho liên tục và xác định nên ta có hàm số đã cho đạt giá trị lớn nhất tại x = 1trên đoạn [-2; 2] khi và chỉ khi 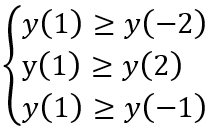⇔ m ≥ 0 ⇒m > 0 (do m ≠ 0).

Câu 10: Tìm tất cả các giá trị thực của tham số m để hàm số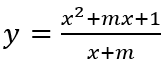 liên tục và đạt giá trị nhỏ nhất trên [0; 2] tại một điểm x₀ ∈ (0; 2).

A. 0 < m < 1.    B. m > 1.    C. m > 2.    D. -1 < m < 1.

Lời giải:

Đáp án : A

Giải thích :

Điều kiện: x ≠ -m. Ta có:

y' = 0 ⇔ (x + m)² = 1 ⇔

Do hệ số x² là số dương và theo yêu cầu đề bài ta có bảng biến thiên như sau:

Hàm số đạt giá trị nhỏ nhất tại x₀ = 1 - m ∈ (0; 2) nên 0 < -m + 1 < 2 ⇔ -1 < m < 1.

Kết hợp điều kiện để hàm số liên tục trên [0; 2] thì -m ∉ [0; 2] ⇔

Ta được : 0 < m < 1.

Câu 11: Với giá trị nào của m thì hàm số 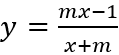đạt giá trị lớn nhất bằng 1/3 trên [0; 2].

A. m = -1.    B. m = 1.    C. m = -3.    D. m = 3.

Lời giải:

Đáp án : B

Giải thích :

Ta có, 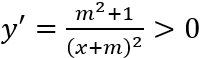,∀ x ≠ -m. Suy ra, hàm số đồng biến trên từng khoảng xác định.

Để hàm số 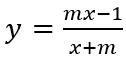đạt giá trị lớn nhất bằng 1/3 trên [0; 2] thì

Câu 12: Giá trị lớn nhất của hàm số 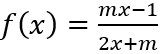trên đoạn [3;5] bằng 2 khi và chỉ khi:

A. m = 7.     B. m ∈ {7; 13}.    C. m ∈ ∅.    D. m = 13.

Lời giải:

Đáp án : A

Giải thích :

Tập xác định: D = R\{-m/2}.

Để hàm số có giá trị lớn nhất trên đoạn [3; 5] thì

Ta có (thỏa đk).