Trong không gian Oxyz, cho đường thẳng d: x-1/1 = y-1/1 = z-m/2

Câu 1:

Trong không gian với hệ tọa độ Oxyz, cho điểm M(1;2;3). Mặt phẳng (P) đi qua M và cắt các tia Ox, Oy, Oz lần lượt tại các điểm A, B, C $\left(A,B,C\ne 0\right)$ sao cho thể tích của tứ diện OABC nhỏ nhất. Phương trình của mặt phẳng (P) là:

Xem lời giải »

Câu 2:

Trong hệ tọa độ Oxyz, cho hai điểm A(1;5;0), B(3;3;6) và đường thẳng $\left(d\right):\left\{\begin{array}{c}x=-1+2t\\ y=1-t\\ z=2t\end{array}\right.$. Một điểm M thay đổi trên d. Biết giá trị nhỏ nhất của nửa chu vi tam giác MAB là số có dạng $\sqrt{a}+\sqrt{b}$ với a, b là các số nguyên. Khi đó:

Xem lời giải »

Câu 3:

Trong không gian Oxyz, cho điểm M(1;3;-2). Hỏi có bao nhiêu mặt phẳng (P) đi qua M và cắt các trục x’Ox, y’Oy, z’Oz lần lượt tại ba điểm phân biệt A, B, C sao cho $OA=OB=OC\ne 0$

Xem lời giải »

Câu 4:

Trong không gian Oxyz, cho mặt cầu (S): $x^2+y^2+z^2-2x-4y+6z-13=0$ và đường thẳng $d:\frac{x+1}{1}=\frac{y+2}{1}=\frac{z-1}{1}$. Tọa độ điểm M trên đường thẳng d sao cho từ M kẻ được 3 tiếp tuyến MA, MB, MC đến mặt cầu (S) (A, B, C là các tiếp điểm) thỏa mãn $\widehat{AMB}=60°,\widehat{BMC}=90°;\widehat{CMA}=120°$ có dạng M(a;b;c) với a < 0. Tổng $a+b+c$ bằng:

Xem lời giải »

Câu 5:

Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA=2a và vuông góc với mặt phẳng đáy. Gọi M là trung điểm cạnh SD. Tang của góc tạo bởi hai mặt phẳng (AMC) và (SBC) bằng:

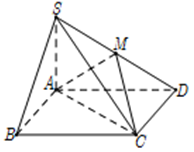
Xem lời giải »

Câu 6:

Cho hình lập phương ABCD.A’B’C’D’ cạnh a. Gọi M, N lần lượt là trung điểm của AC và B’C’. Khoảng cách giữa hai đường thẳng MN và B’D’ bằng:

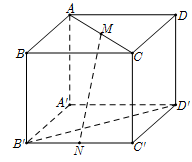
Xem lời giải »

Câu 7:

Trong không gian Oxyz, cho mặt phẳng $\left(\alpha \right):x-z-3=0$ và điểm M(1;1;1). Gọi A là điểm thuộc tia Oz, B là hình chiếu của A lên $\left(\alpha \right)$. Biết rằng tam giác MAB cân tại M. Diện tích của tam giác MAB là:

Xem lời giải »

Câu 8:

Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng (ABCD). Gọi G là trọng tâm của tam giác SAB và M, N lần lượt là trung điểm của SC, SD. Tính cô sin của góc giữa hai mặt phẳng (GMN) và (ABCD)

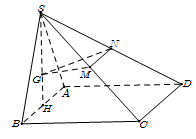
Xem lời giải »