Câu hỏi:
Trong không gian Oxyz, cho đường thẳng và mặt phẳng (P):2x-3y+z-6=0. Phương trình nào dưới đây là phương trình của đường thẳng nằm trong mặt phẳng (P), cắt và vuông góc với (d)?
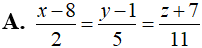
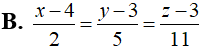
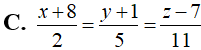
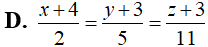
Trả lời:
Chọn A
Phương trình tham số của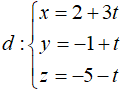 
Gọi M = d ∩ (P) nên 2(2 + 3t) -3(-1 + t) -5 - t - 6 = 0 t = 2 => M (8 ; 1 ; -7)
VTCP của Δ là
Δ đi qua M có VTCP có tọa độ là (2; 5; 11) nên có phương trình:
Câu 1:
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S): (x-1)²+ (y-2)²+ (z-3)²=9 và đường thẳng . Phương trình mặt phẳng (P) đi qua điểm M (4;3;4) song song với đường thẳng ∆ và tiếp xúc với mặt cầu (S) là:
Câu 2:
Trong không gian với hệ tọa độ Oxyz, cho các điểm M (2;2; -3) và N (-4; 2; 1). Gọi Δ là đường thẳng đi qua M, nhận vecto làm vectơ chỉ phương và song song với mặt phẳng (P): 2x + y + z = 0 sao cho khoảng cách từ N đến Δ đạt giá trị nhỏ nhất. Biết |a|, |b| là hai số nguyên tố cùng nhau. Khi đó |a| + |b| + |c| bằng:
Câu 3:
Trong không gian Oxyz, cho hai điểm A (1;0;0), B (0;0;2) và mặt cầu (S): x²+y²+z²-2x-2y+1=0. Hỏi có tất cả bao nhiêu mặt phẳng chứa hai điểm A, B và tiếp xúc với (S).
Câu 4:
Trong không gian Oxyz cho A (1;2;-1), B (3;1;-2), C (2;3;-3) và mặt phẳng (P): x-2y+2z-3=0. M (a;b;c) là điểm thuộc mặt phẳng (P) sao cho biểu thức MA²+MB²+MC² có giá trị nhỏ nhất. Xác định a+b+c.
