Trong không gian Oxyz, cho hai điểm A(10;6;-2), B(5;10;-9) và mặt phẳng
Câu hỏi:
Trong không gian Oxyz, cho hai điểm A(10;6;-2), B(5;10;-9) và mặt phẳng . Điểm M di động trên mặt phẳng sao cho MA, MB luôn tạo với các góc bằng nhau. Biết rằng M luôn thuộc một đường tròn cố định. Hoành độ của tâm đường tròn bằng:
A.
B. 2
C. 10
D. 4
Trả lời:

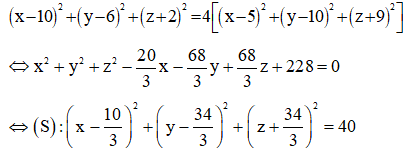

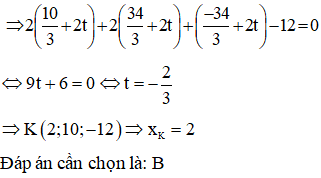
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Trong không gian với hệ tọa độ Oxyz, cho điểm M(1;2;3). Mặt phẳng (P) đi qua M và cắt các tia Ox, Oy, Oz lần lượt tại các điểm A, B, C sao cho thể tích của tứ diện OABC nhỏ nhất. Phương trình của mặt phẳng (P) là:
Xem lời giải »
Câu 2:
Trong hệ tọa độ Oxyz, cho hai điểm A(1;5;0), B(3;3;6) và đường thẳng . Một điểm M thay đổi trên d. Biết giá trị nhỏ nhất của nửa chu vi tam giác MAB là số có dạng với a, b là các số nguyên. Khi đó:
Xem lời giải »
Câu 3:
Trong không gian Oxyz, cho điểm M(1;3;-2). Hỏi có bao nhiêu mặt phẳng (P) đi qua M và cắt các trục x’Ox, y’Oy, z’Oz lần lượt tại ba điểm phân biệt A, B, C sao cho
Xem lời giải »
Câu 4:
Trong không gian Oxyz, cho mặt cầu (S): và đường thẳng . Tọa độ điểm M trên đường thẳng d sao cho từ M kẻ được 3 tiếp tuyến MA, MB, MC đến mặt cầu (S) (A, B, C là các tiếp điểm) thỏa mãn có dạng M(a;b;c) với a < 0. Tổng bằng:
Xem lời giải »
Câu 5:
Trong không gian Oxyz, cho mặt phẳng , đường thẳng và điểm . Gọi là đường thẳng nằm trong mặt phẳng , song song với d đồng thời cách d một khoảng bằng 3. Đường thẳng cắt mặt phẳng (Oxy) tại điểm B. Độ dài đoạn thẳng AB bằng:
Xem lời giải »
Câu 6:
Trong không gian với hệ tọa độ Oxyz, cho M(3;2;1). Mặt phẳng (P) đi qua M và cắt các trục tọa độ Ox, Oy, Oz tại A, B, C sao cho M là trọng tâm tam giác ABC. Phương trình mặt phẳng (P) là:
Xem lời giải »
Câu 7:
Trong không gian với hệ tọa độ Oxyz, cho ba điểm . Gọi M là điểm thay đổi trên mặt phẳng (ABC) và N là điểm trên tia OM sao cho OM.ON=1. Biết rằng N luôn thuộc mặt cầu cố định. Viết phương trình mặt cầu đó?
Xem lời giải »
Câu 8:
Trong không gian Oxyz, mặt phẳng (P): 2x+6y+z-3 = 0 cắt trục Oz và đường thẳng lần lượt tại A và B. Phương trình mặt cầu đường kính AB là:
Xem lời giải »

