Trong không gian Oxyz, cho hai điểm M (2;2;1) ; N ( -8/3 ; 4/3; 8/3)
Câu hỏi:
Trong không gian Oxyz, cho hai điểm M (2;2;1), . Viết phương trình mặt cầu có tâm là tâm của đường tròn nội tiếp tam giác OMN và tiếp xúc với mặt phẳng (Oxz).
A. x²+ (y+1)²+ (z+1)²=1.
B. x²+ (y-1)²+ (z-1)²=1
C. (x-1)²+ (y-1)²+z²=1
D. (x-1)²+y²+ (z-1)²=1.
Trả lời:
Chọn B
Gọi I là tâm đường tròn nội tiếp tam giác OMN.
Ta áp dụng tính chất sau: “Cho tam giác OMN với I là tâm đường tròn nội tiếp, ta có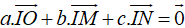 
với a = MN, b = ON, c = OM.
Ta có:
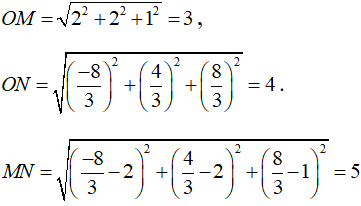
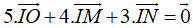
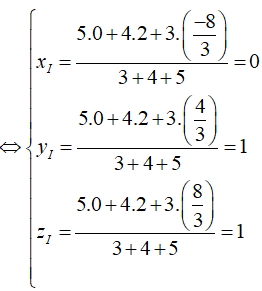
Mặt phẳng (Oxz) có phương trình y = 0.
Mặt cầu tiếp xúc với mặt phẳng (Oxz) nên mặt cầu có bán kính R = d (I, (Oxz)) = 1.
Vậy phương trình mặt cầu là x²+ (y-1)²+ (z-1)²=1.
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Trong không gian với hệ tọa độ Oxyz, cho điểm M (2;1;1). Viết phương trình mặt phẳng (P) đi qua M và cắt ba tia Ox, Oy, Oz lần lượt tại các điểm A, B, C khác gốc O sao cho thể tích khối tứ diện OABC nhỏ nhất.
Xem lời giải »
Câu 2:
Trong không gian Oxyz, Cho mặt phẳng (R): x+y-2z+2=0 và đường thẳng .Đường thẳng Δ2 nằm trong mặt phẳng (R) đồng thời cắt và vuông góc với đường thẳng Δ1 có phương trình là:
Xem lời giải »
Câu 3:
Trong không gian Oxyz, mặt phẳng (α) đi qua M (1;1;4) cắt các tia Ox, Oy, Oz lần lượt tại A, B, C phân biệt sao cho tứ diện OABC có thể tích nhỏ nhất. Tính thể tích nhỏ nhất đó.
Xem lời giải »
Câu 4:
Trong không gian Oxyz, cho đường thẳng và mặt phẳng (P): 2x-y-2z+1=0. Đường thẳng nằm trong (P), cắt và vuông góc với d có phương trình là:
Xem lời giải »
Câu 5:
Có bao nhiêu mặt cầu (S) có tâm thuộc đường thẳng đồng thời tiếp xúc với hai mặt phẳng (α1): 2x+2y+z-6=0 và (α2): x-2y+2z=0
Xem lời giải »
