Trong không gian Oxyz, mặt phẳng (anpha) đi qua M (1;1;4) cắt các tia Ox, Oy, Oz
Câu hỏi:
Trong không gian Oxyz, mặt phẳng (α) đi qua M (1;1;4) cắt các tia Ox, Oy, Oz lần lượt tại A, B, C phân biệt sao cho tứ diện OABC có thể tích nhỏ nhất. Tính thể tích nhỏ nhất đó.
A. 72.
B. 108
B. 18.
D. 36.
Trả lời:
Chọn B
Đặt A= (a;0;0), B= (0;b;0), C= (0;0;c) với a, b, c>0.
Khi đó phương trình mặt phẳng (α) là 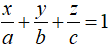
Vì (α) đi qua M (1;1;4) nên 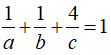
Thể tích của tứ diện OABC là 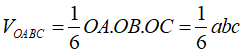
Áp dụng bất đẳng thức AM - GM ta có 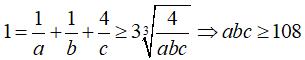
Dấu bằng xảy ra khi a=b=3 ; c=12.
Vậy tứ diện OABC có thể tích nhỏ nhất bằng 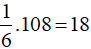
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Trong không gian với hệ tọa độ Oxyz, cho điểm M (2;1;1). Viết phương trình mặt phẳng (P) đi qua M và cắt ba tia Ox, Oy, Oz lần lượt tại các điểm A, B, C khác gốc O sao cho thể tích khối tứ diện OABC nhỏ nhất.
Xem lời giải »
Câu 2:
Trong không gian Oxyz, cho hai điểm M (2;2;1), . Viết phương trình mặt cầu có tâm là tâm của đường tròn nội tiếp tam giác OMN và tiếp xúc với mặt phẳng (Oxz).
Xem lời giải »
Câu 3:
Trong không gian Oxyz, Cho mặt phẳng (R): x+y-2z+2=0 và đường thẳng .Đường thẳng Δ2 nằm trong mặt phẳng (R) đồng thời cắt và vuông góc với đường thẳng Δ1 có phương trình là:
Xem lời giải »
Câu 4:
Trong không gian Oxyz, cho đường thẳng và mặt phẳng (P): 2x-y-2z+1=0. Đường thẳng nằm trong (P), cắt và vuông góc với d có phương trình là:
Xem lời giải »
Câu 5:
Có bao nhiêu mặt cầu (S) có tâm thuộc đường thẳng đồng thời tiếp xúc với hai mặt phẳng (α1): 2x+2y+z-6=0 và (α2): x-2y+2z=0
Xem lời giải »
Câu 6:
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A (1;0;1), B (0;1;-1). Hai điểm D, E thay đổi trên các đoạn OA, OB sao cho đường thẳng DE chia tam giác OAB thành hai phần có diện tích bằng nhau. Khi DE ngắn nhất thì trung điểm của đoạn DE có tọa độ là:
Xem lời giải »
Câu 7:
Trong hệ tọa độ Oxyz cho A (3;3;0), B (3;0;3), C (0;3;3). Mặt phẳng (P) đi qua O, vuông góc với mặt phẳng (ABC) sao cho mặt phẳng (P) cắt các cạnh AB, AC tại các điểm M, N thỏa mãn thể tích tứ diện OAMN nhỏ nhất. Mặt phẳng (P) có phương trình:
Xem lời giải »

