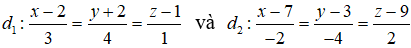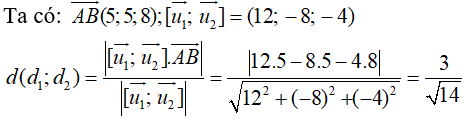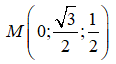Trong không gian Oxyz, cho hai đường thẳng: Cho M là một điểm di động trên d1
Câu hỏi:
Trong không gian Oxyz, cho hai đường thẳng:
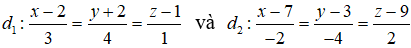
Cho M là một điểm di động trên , N là một điểm di động trên . Khoảng cách nhỏ nhất của đoạn thẳng MN là:
A.
B.
C.
D. 0
Trả lời:
Đáp án B
* Với M là một điểm di động trên , N là một điểm di động trên thì MN d(; )
Do đó, khoảng cách nhỏ nhất của MN chính là khoảng cách giữa hai đường thẳng và . Khi đó, MN là đoạn vuông góc chung của hai đường thẳng đã cho.
* Đường thẳng đi qua A(2; -2; 1), vecto chỉ phương (3; 4; 1)
Đường thẳng đi qua B(7;3;9) vecto chỉ phương (-2; -4; 2)
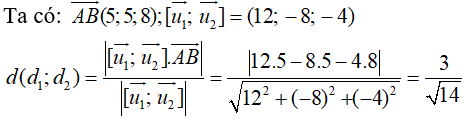
Chọn B.
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Một hình chóp có 40 cạnh. Hình chóp đó có bao nhiêu mặt?
Xem lời giải »
Câu 5:
Trong không gian Oxyz, cho hai điểm A(3;2;1), M(3;0;0) và mặt phẳng (P) có phương trình là: x + y + z - 3 = 0. Viết phương trình của đường thẳng d đi qua điểm M, nằm trong mặt phẳng (P) sao cho khoảng cách từ A đến đường thẳng d lớn nhất
Xem lời giải »
Câu 6:
Cho một đồ chơi hình khối chóp S.ABC có SA, SB, SC đôi một vuông góc với nhau và SA = SB = SC = 6cm. Trong tất cả các khối cầu có thể chứa đồ chơi đó thì khối cầu có bán kính nhỏ nhất là:
Xem lời giải »
Câu 7:
Trong không gian Oxyz, cho mặt cầu (S) có phương trình = 1. Viết phương trình mặt phẳng (P) đi qua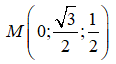 
và tiếp xúc với (S)
Xem lời giải »
