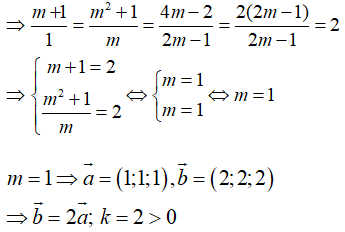Trong không gian Oxyz, cho hai vectơ a = (1; m; 2m - 1), b = (m + 1; m^2 + 1; 4m - 2)
Câu hỏi:
Trong không gian Oxyz, cho hai vectơ = (1; m; 2m - 1), = (m + 1; + 1; 4m - 2). Với những giá trị nào của m thì cos(, ) đạt giá trị lớn nhất?
A. m = 1/2
B. m = 1 hoặc m = 1/2
C. m = 1
D. Không tồn tại m thỏa mãn
Trả lời:
Đáp án C
cos(; ) đạt giá trị lớn nhất khi và chỉ khi góc giữa hai vecto và là 00, nghĩa là tồn tại một số dương k sao cho = k
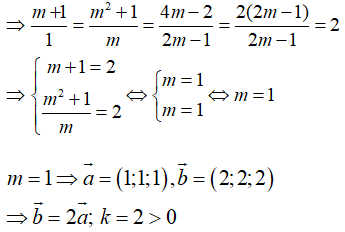
Vậy m = 1 thì thỏa mãn yêu cầu bài toán.
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Trong không gian Oxyz , cho vectơ = (2; 1; -2). Tìm tọa độ của các vectơ cùng phương với vectơ và có độ dài bằng 6.
Xem lời giải »
Câu 2:
Trong không gian Oxyz, cho hai vectơ
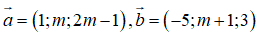
Với những giá trị nào của m thì sinđạt giá trị lớn nhất
Xem lời giải »
Câu 3:
Trong không gian Oxyz, gọi φ là góc tạo bởi hai vectơ = (4; 3; 1); = (-1; 2; 3). Trong các khẳng định sau, khẳng định nào đúng?
Xem lời giải »
Câu 4:
Trong không gian Oxyz , cho hình bình hành ABDC với A(0;0;0), B(1;-2;3), D(3;1;-4). Tọa độ của điểm C là:
Xem lời giải »