Câu hỏi:
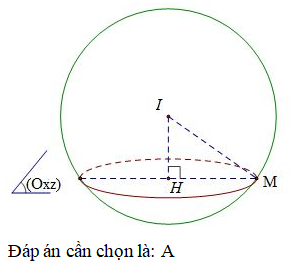
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) có tâm I thuộc đường thẳng Δ:x1=y+31=z2. Biết rằng mặt cầu (S) có bán kính bằng 2√2 và cắt mặt phẳng (Oxz) theo một đường tròn có bán kính 2. Tìm tọa độ tâm I.
A. I(1;−2;2),I(5;2;10)
B. I(1;−2;2),I(0;3;0)
C. I(5;2;10),I(0;−3;0)
D. I(1;−2;2),I(−1;2;−2)
Trả lời:
Câu 1:
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S):x2+(y+1)2+z2=R2. Điều kiện của bán kính R để trục Ox tiếp xúc với (S) là:
Câu 2:
Trong không gian với hệ tọa độ Oxyz, cho điểm I(3;4;-2). Lập phương trình mặt cầu tâm I và tiếp xúc với trục Oz.
Câu 3:
Trong không gian với hệ tọa độ Oxyz, cho điểm A(1;-2;3) và đường thẳng d có phương trình x+12=y−21=z+3−1. Tính đường kính của mặt cầu (S) có tâm A và tiếp xúc với đường thẳng d.
Câu 4:
Trong không gian Oxyz, cho điểm A(1;-2;3) và đường thẳng d có phương trình {x=−1+2ty=2+tz=−3−t(t∈R). Mặt cầu (S) có tâm A và tiếp xúc với đường thẳng d có bán kính là:
Câu 5:
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) có phương trình: (S):x2+y2+z2−2x+4y−2z−3=0 và đường thẳng Δ:x2=y+1−2=z. Mặt phẳng (P) vuông góc với Δ và tiếp xúc với (S) có phương trình là
