Vị trí tương đối của hai mặt cầu: x^2 + y^2 + z^2 + 2x - 2y - 2z - 7 = 0 và

Câu 1:

Trong không gian Oxyz, cho hai vectơ $\overrightarrow{\mathrm{a}}$ = (1; -2; 2), $\overrightarrow{\mathrm{b}}$ = (-2; m - 3; m). Với những giá trị nào của m thì hai vectơ $\overrightarrow{\mathrm{a}}$ và $\overrightarrow{\mathrm{b}}$ có độ dài bằng nhau?

Xem lời giải »

Câu 2:

Trong không gian Oxyz, cho điểm G(1;2;3) là trọng tâm của tam giác ABC trong đó A thuộc trục Ox, B thuộc trục Oy, C thuộc trục Oz. Tọa độ các điểm A, B, C là:

Xem lời giải »

Câu 3:

Trong không gian Oxyz, ba điểm nào dưới đây lập thành ba đỉnh của một tam giác?

Xem lời giải »

Câu 4:

Cho hai vectơ $\overrightarrow{\mathrm{a}}, \overrightarrow{\mathrm{b}}$ thay đổi nhưng luôn thỏa mãn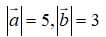 

Giá trị lớn nhất của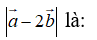

Xem lời giải »

Câu 5:

Trong không gian Oxyz, cho A(1;0;-3), B(-3;-2;-5). Biết rằng tập hợp các điểm M trong không gian thỏa mãn đẳng thức ${\mathrm{AM}}^2 + {\mathrm{BM}}^2$ = 30 là một mặt cầu (S). Tìm tọa độ tâm I và bán kính R của (S).

Xem lời giải »

Câu 6:

Trong không gian Oxyz, cho hai điểm A(0;2;-4), B(-3;5;2). Tìm tọa độ điểm M sao cho biểu thức ${\mathrm{AM}}^2+ 2{\mathrm{BM}}^2$ đạt giá trị nhỏ nhất.

Xem lời giải »

Câu 7:

Trong không gian Oxyz, cho mặt cầu (S) có phương trình là: ${(\mathrm{x} - 1)}^2 + {(\mathrm{y} - 1)}^2 + {(\mathrm{z} - 3)}^2$ = 4

Cho ba điểm A, M, B nằm trên mặt cầu (S) thỏa mãn điều kiện góc AMB = 90^o. Diện tích tam giác AMB có giá trị lớn nhất là:

Xem lời giải »

Câu 8:

Trong không gian Oxyz, cho hai mặt cầu (S) và (S’) có tâm lần lượt là I(-1;2;3), I’(3;-2;1) và có bán kính lần lượt là 4 và 2. Cho điểm M di động trên mặt cầu (S), N di động trên mặt cầu (S’). Khi đó giá trị lớn nhất của đoạn thẳng MN bằng:

Xem lời giải »