Xem hình vẽ, cho biết a// b và c vuông góc a. a) Đường thẳng c
Câu hỏi:
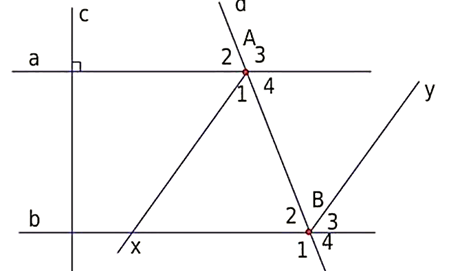
Xem hình vẽ, cho biết a// b và c ⊥ a.
a) Đường thẳng c có vuông góc với đường thẳng b không? Vì sao?
b) Cho đường thẳng d cắt hai đường thẳng a và b tại A và B. Cho biết \(\widehat {{A_1}} = 115^\circ \). Tính số đo các góc \(\widehat {{B_2}};\widehat {{B_3}};\widehat {{A_3}}\).
c) Gọi Ax và By lần lượt là tia phân giác của các góc \(\widehat {{A_1}}\) và \(\widehat {{B_3}}\). Chứng minh: Ax //By.
Trả lời:
a) Vì a // b và c ⊥ a nên c ⊥ b
b) Ta có: a // b nên \(\widehat {{B_2}} + \widehat {{A_1}} = 180^\circ \)(2 góc trong cùng phía)
Suy ra: \(\widehat {{B_2}} = 180^\circ - \widehat {{A_1}} = 180^\circ - 115^\circ = 65^\circ \)
\(\widehat {{B_3}} = \widehat {{A_1}} = 115^\circ \)(2 góc so le trong)
\(\widehat {{A_3}} = \widehat {{A_1}} = 115^\circ \)
c) Ta có: \(\widehat {xAB} = \frac{1}{2}\widehat {{A_1}}\)(vì Ax là phân giác của \(\widehat {{A_1}}\))
\(\widehat {yBA} = \frac{1}{2}\widehat {{B_3}}\)(vì Ax là phân giác của \(\widehat {{B_3}}\))
Mà \(\widehat {{B_3}} = \widehat {{A_1}} = 115^\circ \) nên \(\widehat {xAB} = \widehat {yBA}\)
Mà 2 góc \(\widehat {xAB},\widehat {yBA}\)ở vị trí so le trong nên Ax // By.

