26 bài tập trắc nghiệm Số phức cơ bản chọn lọc, có đáp án - Toán lớp 12

---

26 bài tập trắc nghiệm Số phức cơ bản chọn lọc, có đáp án

Với 26 bài tập trắc nghiệm Số phức cơ bản chọn lọc, có đáp án Toán lớp 12 tổng hợp 26 bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Số phức từ đó đạt điểm cao trong bài thi môn Toán lớp 12.

Câu 1:Cho số phức z = 5 - 4i. Môđun của số phức z là

A.3        B.√41.        C. 1.        D. 9.

Lời giải:

Đáp án : B

Giải thích :

+z = 5 - 4i có a = 5; b = -4

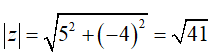
Câu 2:Cho số phức z = 5 - 6i. Số phức liên hợp của z là

A. z = 5 + 6i         B.z = -5 + 6i        C.z = -5 - 6i        D.z = 6 - 5i

Lời giải:

Đáp án : A

Giải thích :

Với z = 5 - 6i thì số phức liên hợp của z là:

z = 5 + 6i

Câu 3:Cho hai số phức z₁ = 1 + 2i; z₂ = 2 - 3i . Phần ảo của số phức w = 3z₁ - 2z₂ là

A. 12.         B. 11.         C. 1.         D.12i

Lời giải:

Đáp án : A

Giải thích :

w = 3z₁ - 2z₂ = 3(1 + 2i) - 2(2 - 3i) = 3 + 6i - 4 + 6i = -1 + 12i

Vậy phần ảo của số phức z là .

Câu 4: Số phức 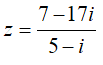có phần thực là

A. 2. B. 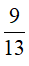. C. 3. D. -3 .

Lời giải:

Đáp án : A

Giải thích :

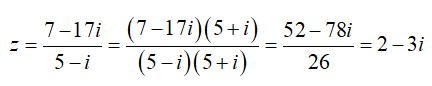
=> phần thực của z là 2

Câu 5: Cho số phức z = 3 + 4i. Khẳng định nào sau đây là khẳng định sai?

A. Điểm biểu diễn của z là M(3;4).

B. Môđun của số phức z là 5.

C. Số phức đối của z là -3 - 4i.

D. Số phức liên hợp của z là 3 - 4i.

Lời giải:

Đáp án : A

Giải thích :

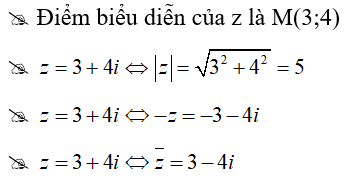
Câu 6:Số nào trong các số phức sau là số thuần ảo?

Lời giải:

Đáp án : C

Giải thích :

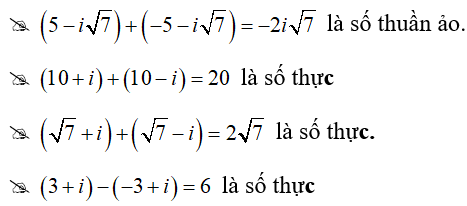
Câu 7:Cho số phức z = 1 + i. Khẳng định nào sau đây là khẳng định đúng?

A. 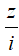= -1 + i .         B. z^-1z .         C.|z|=2         D. z² = 2i.

Lời giải:

Đáp án : D

Giải thích :

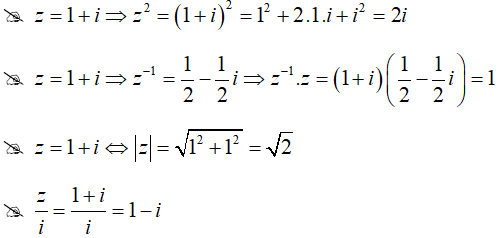
Câu 8:Phần thực, phần ảo của số phức z thỏa mãn 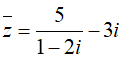lần lượt là

A. 1;1.         B.1;-2         C. 1;2.         D.1;-1

Lời giải:

Đáp án : A

Giải thích :

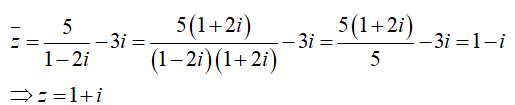
Phần thực, phần ảo của z lần lượt là 1;1.

Câu 9: Cho số phức z thỏa mãn điều kiện:(1 + i)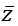 - 1 - 3i = 0. Phần ảo của số phứcw = 1 - iz + z là

A. 1.        B. -3.        C. -2.        D. -1.

Lời giải:

Đáp án : B

Giải thích :

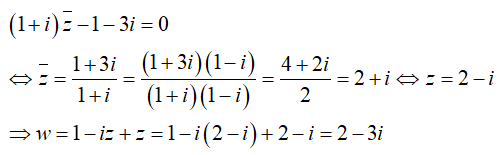
Phần ảo của w là -3

Câu 10: Cho z = 1 - 2i và w = 2 + i. Khẳng định nào sau đây là khẳng định sai?

Lời giải:

Đáp án : A

Giải thích :

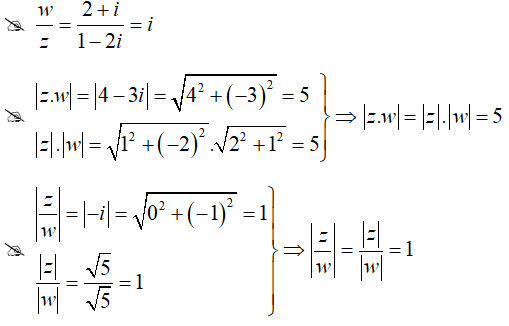
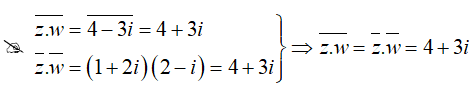
Câu 11:Tìm phần thực, phần ảo của số phức z thỏa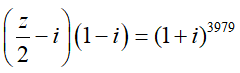

A. Phần thực là 2¹⁹⁹⁰ và phần ảo là 2.

B. Phần thực là -2¹⁹⁹⁰ và phần ảo là 2.

C. Phần thực là -2¹⁹⁸⁹ và phần ảo là 1.

D. Phần thực là 2¹⁹⁸⁹ và phần ảo là 1

Lời giải:

Đáp án : B

Giải thích :

Ta có:

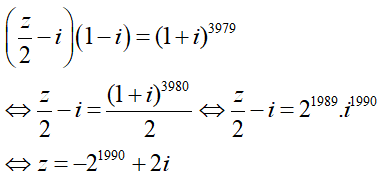
Câu 12:Cho số phức z thỏa . Khi đó phần thực và phần ảo của z = 1 + i + i² + i³ + ... + i²⁰¹⁶ lần lượt là

A.0 và -1.        B. 0 và 1.        C. 1 và 1.        D. 1 và 0.

Lời giải:

Đáp án : D

Giải thích :

Số phức z là tổng của cấp số nhân với số hạng đầu là 1 và công bội q = i . Do đó :

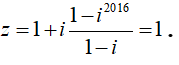
Câu 13:Giá trị của biểu thức S = 1 + i² + i⁴ + ... + i^4k , k ∈ N* là

A. 1.        B. 0.        C.2        D.ik

Lời giải:

Đáp án : A

Giải thích :

Ta có nhận xét sau :

i²ⁿ + i^{2n + 2} = i²ⁿ(1 + i²) = 0, n ∈ N*

Áp dụng tính được

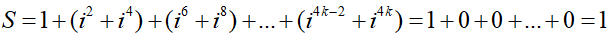
Câu 14:Cho số phức z = 1 + (1 + i) + (1 + i)² + ...+ (1 + i)²⁶ . Phần thực của số phức z là

A. 2¹³        B. -(1 + 2¹³)        C. -2¹³        D. (1 + 2¹³)

Lời giải:

Đáp án : A

Giải thích :

Số phức z là tổng của cấp số nhân với số hạng đầu là 1 và công bội q = 1 + i. Do đó :

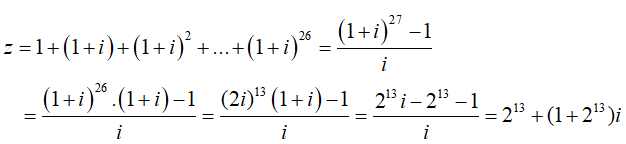
Vậy phần thực là 2¹³

Câu 15: Cho số phức 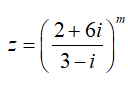,m nguyên dương. Có bao nhiêu giá trị m ∈ [1;50] để z là số thuần ảo?

A. 26.        B. 25.        C. 24.        D. 50.

Lời giải:

Đáp án : B

Giải thích :

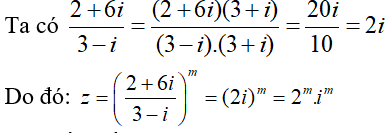
Z là số thuần ảo khi và chỉ khi m = 2k + 1

Mà

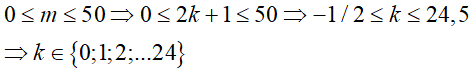
Với 25 giá trị của k cho ta tương ứng 25 giá trị m thỏa yêu cầu đề bài.

Câu 16:Cho số phức z = x + y.i thỏa mãn z³ = 2 - 2i. Cặp số là(x;y)

A.(2; 2)         B.(1;1) .

C.(3;-3)         D.(2; -3)

Lời giải:

Đáp án : B

Giải thích :

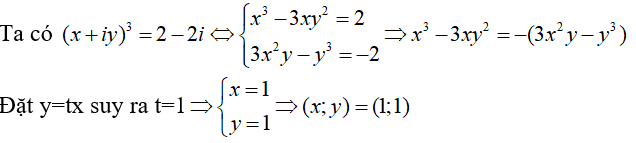
Câu 17:Cho biểu thức 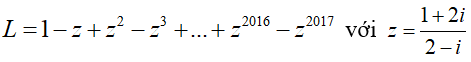. Biểu thức có giá tri là

Lời giải:

Đáp án : A

Giải thích :

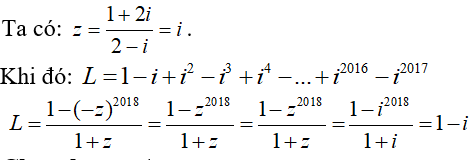
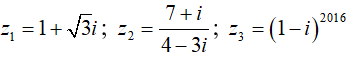
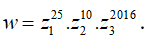
Câu 18:Cho . Tìm dạng đại số của

Lời giải:

Đáp án : B

Giải thích :

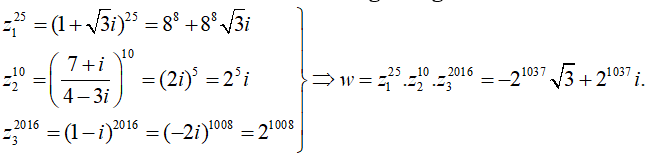
Câu 19:Cho số phức Tìm 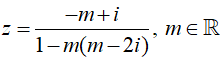|z|_ma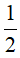x

A. . B. 0.         C. 1.         D. 2.

Lời giải:

Đáp án : A

Giải thích :

Ta có:

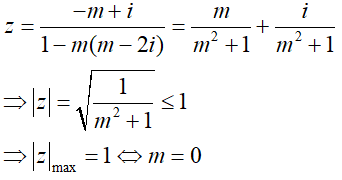
Câu 20:Cho hai số phức z₁ = 1 + 2i ; z₂ = 2 - 3i. Khẳng định nào sau đây là khẳng định sai?

Lời giải:

Đáp án : C

Giải thích :

= 1 - 2i + 8 - i = 9 - 3i

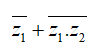
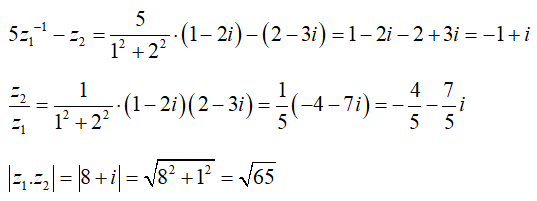
Câu 21:Tính tổng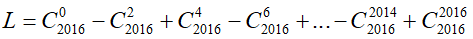

Lời giải:

Đáp án : A

Giải thích :

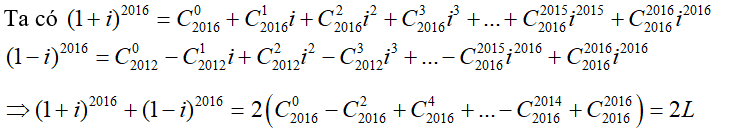
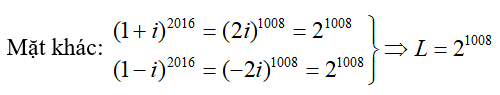
Câu 22:Cho hai số phức z₁;z₂ khác 0 thỏa mãn z₁² - z₁z₂ + z₂² Gọi A,B lần lượt là các điểm biểu diễn cho số phức z₁;z₂. Khi đó tam giác OAB là:

A. Tam giác đều.        B. Tam giác vuông tại O .

C. Tam giác tù.         D. Tam giác có một góc bằng 45^o

Lời giải:

Đáp án : A

Giải thích :

Ta có z₁³ + z₂³ = (z₁ + z₂)(z₁² - z₁z₂ + z₂²)

suy ra:

z₁³ = -z₂³ => |z₁³| = |z₂³| => |z₁| = |z₂| => OA = OB

lại có

(z₁ - z₂)² = (z₁² - z₁z₂ + z₂² - z₁z₂ = -z₁z₂) nên |z₁ - z₂|² = |z₁|.|z₂| => AB² OA.OB = OA²

Suy ra AB = OA = OB => ΔOAB đều

Câu 23: Cho hai số phức z₁ = 1 + i; z₂ = -5 + 2i . Tính môđun của số phức z₁ + z₂.

A. 5.         B.-5.         C.√7.         D.-√7 .

Lời giải:

Đáp án : A

Giải thích :

z₁ + z₂ = (1 + i) + (-5 + 2i) = -4 + 3i

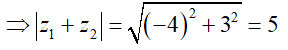
Câu 24: Cho số phức z = (1 - 6i) - (2 - 4i). Phần thực, phần ảo của z lần lượt là

A.-1 ; -2         B. 1 ; 2         C. 2 ; 1.         D. –2 ; 1.

Lời giải:

Đáp án : A

Giải thích :

Ta có z = (1 - 6i) - (2 - 4i) = 1 - 6i - 2 + 4i = -1 - 2i

Câu 25:Giá trị của i¹⁰⁵ + i²⁰ + i²³ - i³⁴ là ?

A.2         B.-2         C.4         D.-4

Lời giải:

Đáp án : A

Giải thích :

Ta có :

i¹⁰⁵ + i²³ + i²⁰ - i³⁴ = i^{4.26 + 1} + i^{4.5 + 3} + i^4.5 - i^{4.8 + 2} = i - i + 1 + 1 = 2

Câu 26:Với mọi số ảo z, số z² + |z|² là:

A. Số thực âm        B. Số 0        C. Số thực dương        D. Số ảo khác 0

Lời giải:

Đáp án : B

Giải thích :

Do z là số ảo nên z có dạng: z = bi.

Ta có: z² + |z²| = (bi)² + b² = -b² + b² = 0.