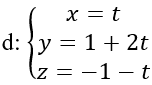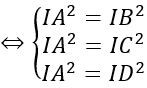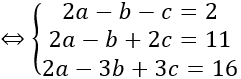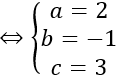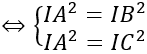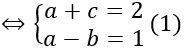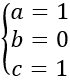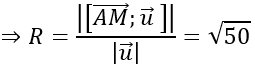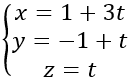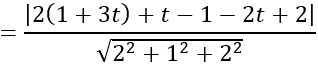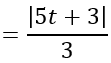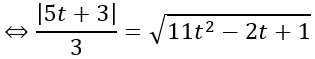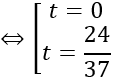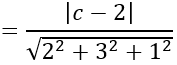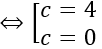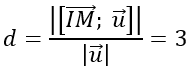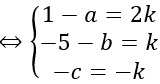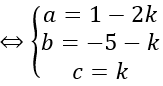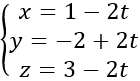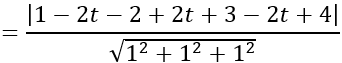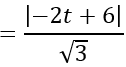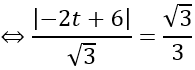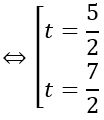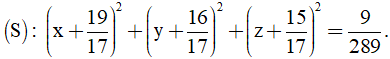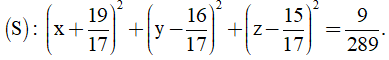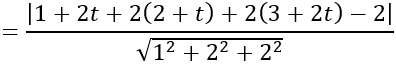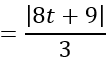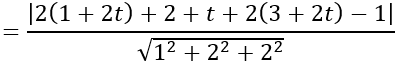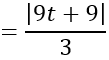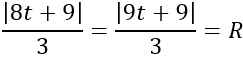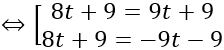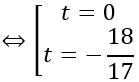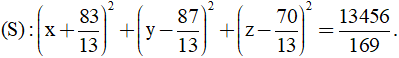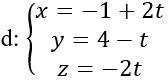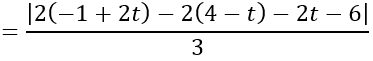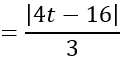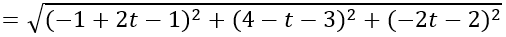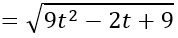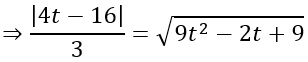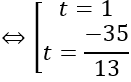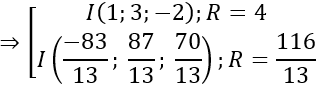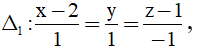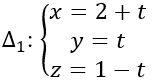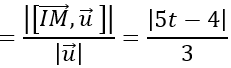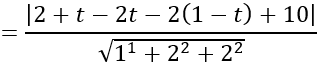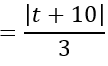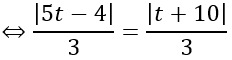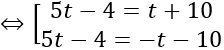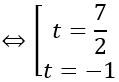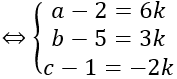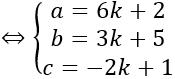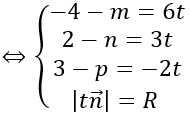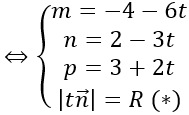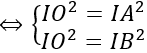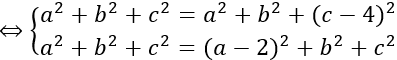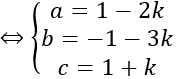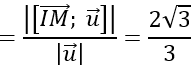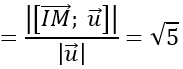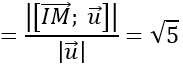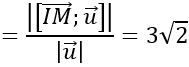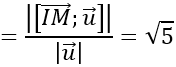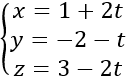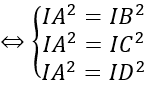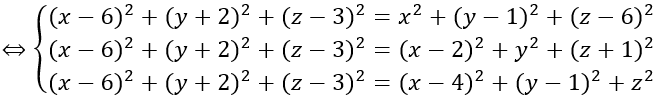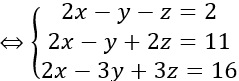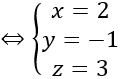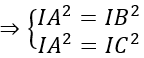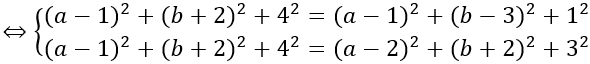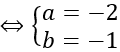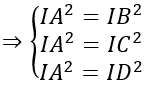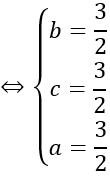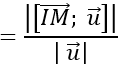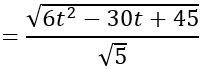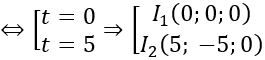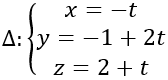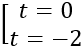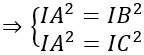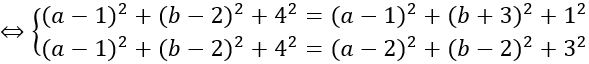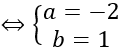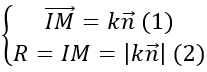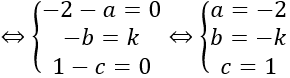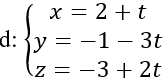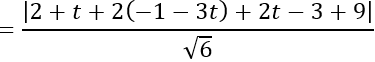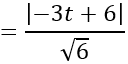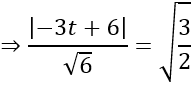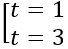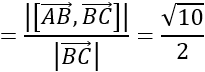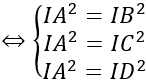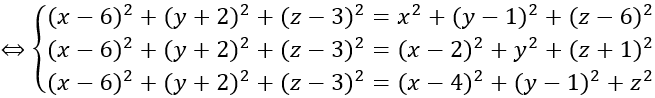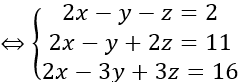60 bài tập trắc nghiệm Viết phương trình mặt cầu chọn lọc, có đáp án - Toán lớp 12
60 bài tập trắc nghiệm Viết phương trình mặt cầu chọn lọc, có đáp án
Với 60 bài tập trắc nghiệm Viết phương trình mặt cầu chọn lọc, có đáp án Toán lớp 12 tổng hợp 60 bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Viết phương trình mặt cầu từ đó đạt điểm cao trong bài thi môn Toán lớp 12.
Bài 1: Cho đường thẳng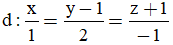 
và điểm A(5;4; - 2). Phương trình mặt cầu đi qua điểm A và có tâm là giao điểm của d với mặt phẳng (Oxy) là:
A. ( S): (x + 1)2 + (y + 1)2 + z2= 65.
B. ( S): ( x + 1)2 + ( y - 1)2 + z2= 9.
C. ( S): (x - 1)2 + (y + 2)2 + z2 = 64.
D. ( S): (x + 1)2 + ( y - 1)2 + (z + 2)2= 65.
Lời giải:
Đáp án : A
Giải thích :
Phương trình tham số của đường thẳng 
Gọi I là tâm của mặt cầu. Do I thuộc d nên I(t;1+2t; -1-t)
Mặt khác do I thuộc mặt phẳng Oxy nên -1-t=0 ⇔ t= -1
Khi đó I (-1; -1; 0)
Mặt cầu đi qua điểm A nên R2 =IA2 =(5+1)2+ (4+1)2 +(-2+0)2=65
Vậy pt mặt cầu cần tìm là: (x+1)2 +(y+1)2 +z2 =65
Bài 2: Cho bốn điểm A(6;-2;3), B(0;1;6), C(2;0;-1), D(4;1;0). Khi đó mặt cầu ngoại tiếp tứ diện ABCD có phương trình là:
A. x2 + y2 + z2 + 4x - 2y + 6z - 3 = 0.
B. x2 + y2 + z2 - 4x + 2y - 6z - 3 = 0.
C. x2 + y2 + z2 - 2x + y - 3z - 3 = 0.
D. x2 + y2 + z2 + 2x - y + 3z - 3 = 0.
Lời giải:
Đáp án : B
Giải thích :
Gọi I (a; b; c) là tâm mặt cầu
Do mặt cầu ngoại tiếp tứ diện ABCD nên IA = IB = IC = ID
Bán kính R = IA = √17
Vậy phương trình mặt cầu cần tìm là
(x-2)2 +(y+1)2 +(z-3)2 =17
⇔ x2 +y2 +z2 -4x +2y -6z -3 =0
Bài 3: Cho ba điểm A(2;0;1), B(1;0;0), C(1;1;1) và mặt phẳng (P): x + y + z - 2 = 0. Phương trình mặt cầu đi qua ba điểm A, B, C và có tâm thuộc mặt phẳng (P) là:
A. x2 + y2 + z2 - 2x + 2y + 1 = 0.
B. x2 + y2 + z2 - x - 2y + 1 = 0.
C. x2 + y2 + z2 - 2x - 2z + 1 = 0.
D. x2 + y2 + z2 - x + 2z + 1 = 0.
Lời giải:
Đáp án : C
Giải thích :
Gọi I (a; b; c) là tâm mặt cầu
Do mặt cầu đi qua 3 điểm A, B, C nên ta có IA = IB = IC
Mặt khác do I thuộc mặt phẳng (P) nên a + b + c – 2 = 0 (2)
Từ (1) và (2) ta có
Bán kính mặt cầu: R=IA=1
Vậy pt mặt cầu là
(x-1)2 +y2 +(z-1)2 =1
⇔ x2 +y2 +z2 -2x -2z +1 =0
Bài 4: Phương trình mặt cầu tâm I(1;-2;3) và tiếp xúc với trục Oy là:
A. (x - 1)2 + (y + 2)2 + (z - 3)2 = 10.
B. (x - 1)2 + (y + 2)2 + (z - 3)2 = 16.
C. (x - 1)2 + (y + 2)2 + (z - 3)2 = 8.
D. (x - 1)2 + (y + 2)2 + (z - 3)2 = 9.
Lời giải:
Đáp án : A
Giải thích :
Chú ý:
Khoảng cách từ điểm I (a; b; c ) đến trục Ox là d= √(b2 +c2 )
Khoảng cách từ điểm I (a; b; c ) đến trục Oy là d= √(a2 +c2 )
Khoảng cách từ điểm I (a; b; c ) đến trục Oz là d= √(a2 +b2 )
Khoảng cách từ I (1; -2; 3) đến Oy là: d= √(12 +32) = √10
Mặt cầu tiếp xúc với Oy nên R = d= √10
Phương trình mặt cầu cần tìm là:
(x-1)2 +(y+2)2 +(z-3)2 =10
Bài 5: Cho các điểm A(-2;4;1), B(2;0;3) và đường thẳng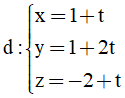 
. Gọi (S) là mặt cầu đi qua A, B và có tâm thuộc đường thẳng d. Bán kính mặt cầu (S) bằng:
A. 2√3 B. √6
C. 3 D. 3√3
Lời giải:
Đáp án : D
Giải thích :
Gọi I là tâm mặt cầu, do I thuộc d nên I(1+t;1+2t; -2+t)
Do mặt cầu đi qua A, B nên IA = IB
⇔ IA2 =IB2
⇔ (t+3)2 +(2t-3)2 +(t-3)2 =(t-1)2 +(2t+1)2 +(t-5)2
⇔ t=0
Khi đó I (1; 1; -2)
Bán kính mặt cầu R=IA= 3√3
Bài 6: Cho điểm A(1;-2;3) và đường thẳng d có phương trình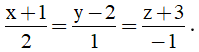 
Phương trình mặt cầu tâm A, tiếp xúc với d là:
A. (x-1)2 + (y + 2)2 + (z-3)2 = √50.
B. (x-1)2 + (y + 2)2 + (z-3)2 = 5.
C. ( x-1)2 + (y + 2)2 + (z-3)2 = 50.
D. (x + 1)2 + (y - 2)2 + (z + 3)2 = 50.
Lời giải:
Đáp án : C
Giải thích :
Đường thẳng d đi qua điểm M (-1; 2; -3) và có vecto chỉ phương
u→=(2;1;-1)
AM→=(-2;4; -6); [AM→ ; u→ ]=(2; -14; -10)
Do mặt cầu tiếp xúc với d nên khoảng cách từ A đến đường thẳng d bằng bán kính R của mặt cầu
Phương trình mặt cầu cần tìm là:
(x-1)2 +(y+2)2 +(z-3)2 =50
Bài 7: Cho đường thẳng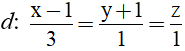 
và mặt phẳng (P): 2x + y - 2z + 2 = 0 Phương trình mặt cầu (S) có tâm nằm trên đường thẳng d có bán kính nhỏ nhất tiếp xúc với (P) và đi qua điểm A(1;-1;1) là:
A. (x - 1)2 + (y + 1)2 + z2 = 1.
B. (x - 4)2 + y2 + (z - 1)2 = 1.
C. (x + 2)2 + (y + 2)2 + (z + 1)2 = 1.
D. (x - 3)2 + (y - 1)2 + (z - 1)2 = 1.
Lời giải:
Đáp án : A
Giải thích :
Phương trình tham số của đường thẳng d là: 
Gọi I là tâm mặt cầu, do I thuộc đường thẳng d nên I(1+3t; -1+t;t)
Khoảng cách từ điểm I đến mặt phẳng (P) là:
d(I;(P))
IA2 =(1+3t-1)2 +(-1+t+1)2 +(t-1)2=11t2 -2t +1
Do mặt cầu tiếp xúc với (P) và đi qua A nên d(I;(P))=IA
⇔ (5t+3)2 =11t2 -2t +1
Với t = 0, ta có I (1; -1; 0), R = IA = 1
Với t=24/37, ta có I(109/37; (-13)/37; 24/37); R =IA =5929/1369
Theo bài ra, cần viết phương trình mặt cầu có bán kính nhỏ nhất nên viết phương trình mặt cầu có tâm I (1; -1; 0), R = 1
(x-1)2 +(y+1)2 +z2 =1
Bài 8: Phương trình mặt cầu có tâm I(1;2;3) và tiếp xúc với mặt phẳng (Oxz) là:
A. x2 + y2 + z2 + 2x + 4y + 6z - 10 = 0.
B. x2 + y2 + z2 - 2x - 4y - 6z + 10 = 0.
C. x2 + y2 + z2 - 2x - 4y + 6z + 10 = 0.
D. x2 + y2 + z2 + 2x + 4y + 6z - 10 = 0.
Lời giải:
Đáp án : B
Giải thích :
Phương trình mặt phẳng (Oxz) là: y = 0
Khoảng cách từ điểm I đến mặt phẳng (Oxz) là: d = 2
Phương trình mặt cầu cần tìm là:
(x-1)2 +(y-2)2 +(z-3)2 =4
⇔ x2 +y2 +z2 -2x -4y -6z +10=0
Bài 9: Cho 4 điềm A(3;-2;-2), B(3;2;0), C(0;2;1), D(-1;1;2). Mặt cầu tâm A và tiếp xúc với mặt phẳng (BCD) có phương trình là:
A. (x - 3)2 + (y + 2)2 + (z + 2)2 = √14.
B. (x + 3)2 + (y - 2)2 + (z - 2)2 = 14.
C. (x + 3)2 + (y - 2)2 + (z - 2)2 = √14.
D. (x - 3)2 + (y + 2)2 + (z + 2)2 = 14.
Lời giải:
Đáp án : D
Giải thích :
BC→=(-3;0;1); BD→=(-4; -1;2)
⇒ [BC→ , BD→ ]=(1;2;3)
⇒ Vecto pháp tuyến của mặt phẳng (BCD) là: n→ =(1;2;3)
Phương trình mặt phẳng (BCD) có VPPT n→=(1;2;3) và đi qua điểm B(3; 2; 0) là: x -3 +2(y-2) +3z =0
⇔ x +2y +3z -7 =0
Khoảng cách từ A đến mặt phẳng (BCD) là:
d(A;(BCD))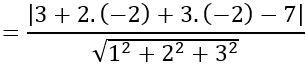
= √14
Khi đó, phương trình mặt cầu tâm A và tiếp xúc với (BCD) là:
(x-3)2 +(y+2)2 +(z+2)2=14
Bài 10: Cho mặt phẳng (P): 2x + 3y + z - 2 = 0. Mặt cầu (S) có tâm I thuộc trục Oz, bán kính bằng 2/(√14) và tiếp xúc mặt phẳng (P) có phương trình:
A. x2 + y2 + (z - 3)2 = 2/7 hoặc x2 + y2 + (z - 4)2 = 2/7.
B. x2 + y2 + (z - 1)2 = 2/7 hoặc x2 + y2 + (z + 2)2 = 2/7.
C. x2 + y2 + z2 = 2/7 hoặc x2 + y2 + (z - 4)2 = 2/7.
D. x2 + y2 + z2 = 2/7 hoặc x2 + y2 + (z - 1)2 = 2/7.
Lời giải:
Đáp án : C
Giải thích :
Tâm I thuộc trục Oz nên I (0; 0; c)
Do mặt cầu tiếp xúc với mặt phẳng (P) nên khoảng cách từ I đến mặt phẳng (P) bằng bán kính mặt cầu
⇒ R=2/√(14)
⇒ |c-2|=2
Vậy I (0; 0; 0) hoặc I (0; 0; 4)
Vậy phương trình mặt cầu cần tìm là
x2 +y2 +z2 =2/7
x2 +y2 +(z-4)2 =2/7
Bài 11: Cho đường thẳng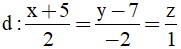 
và điểm I(4;1;6). Đường thẳng d cắt mặt cầu (S) tâm I tại hai điểm A, B sao cho AB=6. Phương trình của mặt cầu (S) là:
A. (x - 4)2 + (y - 1)2 + (z - 6)2 = 18.
B. (x - 4)2 + (y - 1)2 + (z - 6)2 = 12.
C. (x - 4)2 + (y - 1)2 + (z - 6)2 = 16.
D. (x - 4)2 + (y - 1)2 + (z - 6)2 = 9.
Lời giải:
Đáp án : A
Giải thích :
Đường thẳng d đi qua điểm M (-5; 7; 0) và có vecto chỉ phương u→ =(2; -2;1)
IM→ =(-9;6; -6) ⇒ [ IM→ ; u→ ]=(-6; -3;6)
Khoảng cách từ I đến đường thẳng d là :
Gọi R là bán kính của mặt cầu
⇒ R2 =d2 +(AB2)/4=18
Vậy phương trình mặt cầu cần tìm là
(x-4)2 +(y-1)2 +(z-6)2 =18
Bài 12: Cho hai mặt phẳng (P), (Q) có phương trình (P): x - 2y + z - 1 = 0 và (Q): 2x + y - z + 3 = 0. Mặt cầu có tâm nằm trên mặt phẳng (P) và tiếp xúc với mặt phẳng (Q) tại điểm M, biết rằng M thuộc mặt phẳng (Oxy) và có hoành độ XM=1, có phương trình là:
A. (x + 19)2 + (y + 15)2 + (z - 10)2 = 600.
B. (x - 21)2 + (y - 5)2 + (z + 10)2 = 600.
C. (x - 21)2 + (y - 5)2 + (z + 10)2 = 100.
D. (x + 21)2 + (y + 5)2 + (z - 10)2 = 600.
Lời giải:
Đáp án : B
Giải thích :
Điểm M thuộc mặt phẳng Oxy và có hoành độ xM =1 nên M (1; y0; 0)
Mặt khác M thuộc mặt phẳng Q nên 2. 1 + y0 + 3 = 0 ⇒ y0= -5
⇒ M (1; -5;0)
Gọi I (a; b; c) là tâm mặt cầu
⇒ IM→=(1-a; -5-b; -c)
Mặt phẳng (Q) có vecto pháp tuyến n→=(2;1;-1)
Do mặt cầu tiếp xúc với (Q) tại điểm M nên IM→ vuông góc với mặt phẳng (Q)
⇒ IM→=k n→
Mặt khác I thuộc mặt phẳng (P) nên tọa độ của I thỏa mãn phương trình mặt phẳng (P)
⇒ a -2b +c -1 =0
⇔ 1 -2k +2(5+k) +k -1 =0
⇔ k =-10
Với k =-10 thì I (21; 5; -10)
Bán kính của mặt cầu là:
R =|IM→ |=|k n→ |
Vậy phương trình mặt cầu cần tìm là:
(x-21)2 +(y-5)2 +(z+10)2 =600
Bài 13: Cho hai điểm A(1;-2;3), B(-1;0;1) và mặt phẳng (P): x + y + z + 4 = 0. Phương trình mặt cầu (S) có bán kính bằng AB/6 có tâm thuộc đường thẳng AB và (S) tiếp xúc với mặt phẳng (P) là:
A. (x + 4)2 + (y - 3)2 + (z + 2)2 = 1/3 hoặc (x + 6)2 + (y - 5)2 + (z + 4)2 = 1/3.
B. (x - 4)2 + (y + 3)2 + (z - 2)2 = 1/3 hoặc (x - 6)2 + (y + 5)2 + (z - 4)2 = 1/3.
C. (x + 4)2 + (y - 3)2 + (z + 2)2 = 1/3.
D. (x - 4)2 + (y + 3)2 + (z - 2)2 = 1/3.
Lời giải:
Đáp án : C
Giải thích :
AB→=(-2;2;-2) ⇒ AB=|AB→ |= 2√3
Gọi R là bán kính của mặt cầu (S). Theo giả thiết ta có:
R =AB/6 = √3/3
Đường thẳng AB đi qua A (1; -2; 3) và có một vecto chỉ phương
AB→=(-2;2;-2) có phương trình là: 
Tâm I thuộc đường thẳng AB nên I(1-2t; -2+2t; 3-2t)
Khoảng cách từ tâm I đến mặt phẳng (P) là:
d(I; (P))
Do mặt cầu tiếp xúc với (P) nên d(I;(P)) =R
⇔ |-2t+6|=1
Với t=5/2 thì I ( -4; 3; -2)
Với t=7/2 thì I ( -6; 5; -4)
Vậy có 2 phương trình mặt cầu thỏa mãn là :
(x+4)2 +(y-3)2 +(z+2)2 =1/3
(x+6)2 +(y-5)2 +(z+4)2=1/3
Bài 14: Cho đường thẳng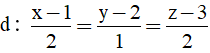 
và hai mặt phẳng (P1): x, + 2y + 2z - 2 = 0; (P2): 2x + y + 2z - 1 = 0. Mặt cầu có tâm I nằm trên d và tiếp xúc với 2 mặt phẳng (P1), (P2) có phương trình:
A. (S): (x + 1)2 + (y + 2)2 + (z + 3)2 = 9.
B. (S): (x + 1)2 + (y + 2)2 + (z + 3)2 = 9 hoặc
C. (S): (x - 1)2 + (y - 2)2 + (z - 3)2 = 9.
D. (S): (x - 1)2 + (y - 2)2 + (z - 3)2 = 9 hoặc
Lời giải:
Đáp án : D
Giải thích :
Do I nằm trên d nên I (1 + 2t; 2 + t; 3 + 2t)
d(I;(P))
d(I;(Q))
Do mặt cầu (S) tiếp xúc với 2 mặt phẳng (P) và (Q) nên
⇔ |8t+9| =|9t+9|
Với t=0 thì I(1;2;3); R=3
Với t= -18/17 thì I(-19/17; 16/17; 15/17); R= 3/17
Vậy có 2 phương trình mặt cầu thỏa mãn đề bài là:
(x-1)2 +(y-2)2 +(z-3)2 =9
(x+19/17)2 +(y-16/17)2 +(z-15/17)2 =9/289
Bài 15: Cho điểm A(1;3;2), đường thẳng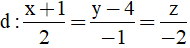 
và mặt phẳng (P): 2x - 2y + z - 6 = 0. Phương trình mặt cầu (S) đi qua A, có tâm thuộc d đồng thời tiếp xúc với (P) là:
A. (S): (x - 1)2 + (y - 3)2 + (z + 2)2 = 16 hoặc
B. (S): (x + 1)2 + (y + 3)2 + (z - 2)2 = 16 hoặc
C. (S): (x - 1)2 + (y - 3)2 + (z + 2)2 = 16.
D. (S): (x - 1)2 + (y - 3)2 + (z + 2)2 = 4.
Lời giải:
Đáp án : A
Giải thích :
Phương trình đường thẳng
Gọi I là tâm mặt cầu, do I thuộc d nên I (-1+2t; 4 – t; -2t)
Khoảng cách từ I đến mặt phẳng (P) là:
d(I;(P)
IA
Do mặt cầu đi qua A và tiếp xúc với (P) nên d(I; (P)) =IA =R
⇔ 65t2 +110t -175 =0
Khi đó, phương trình mặt cầu cần tìm là:
(x-1)2 +(y-3)2 +(z+2)2 =16
(x +83/13)2 +(y -87/13)2 +(z -70/13)2 =13456/169
Bài 16: Cho mặt phẳng (P): x - 2y - 2z + 10 = 0 và hai đường thẳng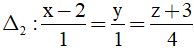 
. Mặt cầu (S) có tâm thuộc Δ1, tiếp xúc với Δ2 và mặt phẳng (P), có phương trình:
A. (x + 1)2 + (y - 1)2 + (z + 2)2 = 9 hoặc (x + 11/2)2 + (y + 7/2)2 + (z - 5/2)2 = 81/4.
B. (x - 1)2 + (y + 1)2 + (z - 2)2 = 9 hoặc (x - 11/2)2 + (y - 7/2)2 + (z + 5/2)2 = 81/4.
C. (x - 1)2 + (y + 1)2 + (z - 2)2 = 9.
D. (x - 1)2 + (y + 1)2 + (z - 2)2 = 3.
Lời giải:
Đáp án : B
Giải thích :
Phương trình tham số của đường thẳng 
Do I thuộc đường thẳng Δ1 nên I ( 2+t; t; 1- t)
Đường thẳng Δ2 đi qua điểm M (2; 0; -3) và có vecto chỉ phương u→ =(1;1;4)
IM→ =(-t; -t;t-4) ⇒ [ IM→ , u→ ] =(4 -5t; 5t -4; 0)
Khoảng cách từ I đến Δ2 là:
d(I; Δ2 )
Khoảng cách từ I đến mặt phẳng (P) là:
d(I;(P))
Theo bài ra, mặt cầu tiếp xúc với Δ1 và mặt phẳng (P) nên:
d(I; Δ1 )= d(I;(P)) =R
⇔ |5t -4| =|t +10|
Với t=7/2, I(11/2; 7/2; (-5)/2), R=9/2
Với t = - 1, I (1; -1; 2); R= 3
Vậy phương trình mặt cầu cần tìm là:
(x -11/2)2 +(y -7/2)2 +(z +5/2)2 =81/4
(x -1)2 +(y +1)2 +(z -2)2 =9
Bài 17: Cho điểm A(2;5;1) và mặt phẳng (P): 6x + 3y - 2z + 24 = 0, H là hình chiếu vuông góc của A trên mặt phẳng (P). Phương trình mặt cầu (S) có diện tích 784π và tiếp xúc với mặt phẳng (P) tại H, sao cho điểm A nằm trong mặt cầu là:
A. (x + 16)2 + (y + 4)2 + (z - 7)2 = 196.
B. (x + 8)2 + (y + 8)2 + (z - 1)2 = 196.
C. (x - 8)2 + (y - 8)2 + (z + 1)2 = 196.
D. (x - 16)2 + (y - 4)2 + (z + 7)2 = 196.
Lời giải:
Đáp án : C
Giải thích :
Gọi H (a; b; c).
⇒ AH→=(a -2; b -5; c -1)
Mặt phẳng (P) có vecto pháp tuyến n→=(6;3;-2)
Do H là hình chiếu vuông góc của A trên mặt phẳng (P) nên AH→ vuông góc với mặt phẳng (P).
⇒ AH→=k n→
Lại có H thuộc (P) nên 6a + 3b – 2c + 24 = 0
⇔ 6(6k+2) +3(3k+5) -2(-2k+1) +24 =0
⇔ k= -1
⇒ H(-4;2;3)
Gọi R là bán kính mặt cầu.
Mặt cầu (S) có diện tích là 784π
⇒ 4π R2=784π ⇒ R=14
Gọi I (m, n, p) là tâm mặt cầu
⇒ IH→=(-4-m; 2-n; 3-p)
Do mặt cầu tiếp xúc với mặt phẳng (P) tại H nên ta có
Xét (*): |t n→ |=R
⇔ |t| =2 ⇔ t =±2
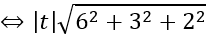
Với t = 2 ta có I (-16; -4; 7)
Khi đó:
= 21 > R
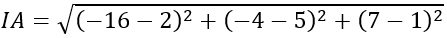
⇒ A nằm ngoài mặt cầu.
Với t = - 2 ta có I (8; 8; -1)
Khi đó:
IA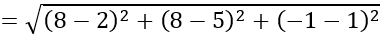
= 7<R
⇒ A nằm trong mặt cầu.
Vậy phương trình mặt cầu cần tìm là:
(x-8)2 +(y-8)2 +(z+1)2 =196
Bài 18: Cho mặt phẳng (P): 2x + y - z + 5 = 0 và các điểm A(0;0;4), B(2;0;0). Phương trình mặt cầu đi qua O, A, B và tiếp xúc với mặt phẳng (P) là:
A. (x - 1)2 + (y - 1)2 + (z - 2)2 = 6.
B. (x + 1)2 + (y + 1)2 + (z + 2)2 = 6.
C. (x - 1)2 + (y + 1)2 + (z - 2)2 = 6.
D. (x - 1)2 + (y - 1)2 + (z + 2)2 = 6.
Lời giải:
Đáp án : A
Giải thích :
Gọi I (a; b; c) là tâm mặt cầu
Lại có mặt cầu đi qua O; A; B nên IO = IA = IB
⇒ I(1;b;2)
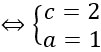
Khoảng cách từ I đến mặt phẳng (P) là:
d(I;(P))
Do mặt cầu tiếp xúc với mặt phẳng (P) nên d(I;(P))=IO
⇔ (b+5)2/6 =5 +b2⇔ 5b2 -10b +5 =0 ⇔ b=1
Vậy I (1; 1; 2) và R = √6
Phương trình mặt cầu cần tìm là:
(x-1)2 +(y-12 +(z-2)2 =6
Bài 19: Cho hai mặt phẳng (P): 2x + 3y - z + 2 = 0, (Q): 2x - y - z + 2 = 0. Phương trình mặt cầu (S) tiếp xúc với mặt phẳng (P) tại điểm A(1;-1;1) và có tâm thuộc mặt phẳng (Q) là:
A. (S): (x - 3)2 + (y - 7)2 + (z + 3)2 = 56.
B. (S): (x + 3)2 + (y + 7)2 + (z - 3)2 = 56.
C. (S): (x + 3)2 + (y + 7)2 + (z - 3)2 = 14.
D. (S): (x - 3)2 + (y - 7)2 + (z + 3)2 = 14.
Lời giải:
Đáp án : B
Giải thích :
Gọi I (a; b; c) là tâm của mặt cầu
⇒ IA→=(1 -a; -1 -b; 1 -c)
Mặt phẳng (P) có vecto pháp tuyến n→=(2;3; -1)
Do mặt cầu tiếp xúc với (P) tại điểm A nên IA→ vuông góc với mặt phẳng (P)
⇒ IA→= k n→
Lại có I thuộc mặt phẳng (Q) nên ta có:
2a -b -c +2 =0
⇔ 2(1 -2k) +(1 +3k) -1 -k +2 =0
⇔ k=2
Với k = 2 thì I (-3; -7; 3)
Bán kính mặt cầu: R=|IA→ | =|k n→ |
= 2√14
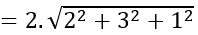
Vậy phương trình mặt cầu cần tìm là:
(x+3)2 +(y+7)2 +(z-3)2 =56
Bài 20: Cho điểm I(0;0;3) và đường thẳng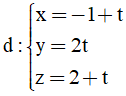
. Phương trình mặt cầu (S) có tâm I và cắt đường thẳng d tại hai điểm A, B sao cho tam giác IAB vuông là:
A. x2 + y2 + (z - 3)2 = 4/3.
B. x2 + y2 + (z - 3)2 = 3/2.
C. x2 + y2 + (z - 3)2 = 2/3.
D. x2 + y2 + (z - 3)2 = 8/3.
Lời giải:
Đáp án : D
Giải thích :
Đường thẳng d đi qua điểm M(-1; 0; 2) và có vecto chỉ phương u→ =(1;2;1)
IM→ =(-1;0; -1) ⇒ [IM→ ; u→ ]=(2;0;-2)
Khoảng cách từ I đến đường thẳng d là
d(I;d)
Tam giác IAB có IA = IB = R, vuông cân tại I nên AB= R√2
Mặt khác ta có: IA. IB = d(I;d).AB
⇔ R2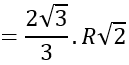
⇔ R=(2√6)/3
Phương trình mặt cầu cần tìm là
x2 +y2 +(z-3)2 =8/3
Bài 21: Cho điểm I(1;0;0) và đường thẳng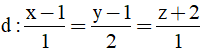 
. Phương trình mặt cầu (S)có tâm I và cắt đường thẳng d tại hai điểm A, B sao cho AB=4 là:
A. (x - 1)2 + y2 + z2 = 9.
B. (x - 1)2 + y2 + z2 = 3.
C. (x + 1)2 + y2 + z2 = 3.
D. (x + 1)2 + y2 + z2 = 9.
Lời giải:
Đáp án : A
Giải thích :
Đường thẳng (d) đi qua điểm M (1; l; -2) và có vecto chỉ phương u→=(1;2;1)
IM→=(0;1; -2) ⇒ [IM→ ; u→ ]=(5; -2; -1)
Khoảng cách từ I đến đường thẳng d là:
h =d(I;d)
Gọi R là bán kính của mặt cầu. Ta có:
R2 =h2 +(AB/2)2 =5 +22 =9
Vậy phương trình mặt cầu cần tìm là:
(x-1)2 +y2 +z2 =9
Bài 22: Cho điểm I(1;0;0) và đường thẳng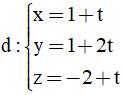 
. Phương trình mặt cầu (S) có tâm I và cắt đường thẳng d tại hai điểm A, B sao cho tam giác IAB đều là:
A. (x - 1)2 + y2 + z2 = 16/4.
B. (x + 1)2 + y2 + z2 = 20/3.
C. (x - 1)2 + y2 + z2 = 20/3.
D. (x - 1)2 + y2 + z2 = 5/3.
Lời giải:
Đáp án : C
Giải thích :
Đường thẳng (d) đi qua điểm M (1; l; -2) và có vecto chỉ phương u→=(1;2;1)
IM→=(0;1; -2) ⇒ [IM→ ; u→ ]=(5; -2; -1)
Khoảng cách từ I đến đường thẳng d là:
h =d(I;d)
Do tam giác IAB đều nên ta có:
h =(IA√3)/2 ⇒ √5=(R√3)/2 ⇒ R=(2√15)/3
Vậy phương trình mặt cầu là
(x-1)2 +y2 +z2 =20/3
Bài 23: Cho điểm I(1;1;-2) đường thẳng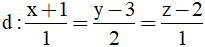
. Phương trình mặt cầu (S) có tâm I và cắt đường thẳng d tại hai điểm A, B sao cho IABˆ = 300 là:
A. (x + 1)2 + (y + 1)2 + (z - 2)2 = 36.
B. (x - 1)2 + y - 1)2 + (z + 2)2 = 72.
C. (x - 1)2 + (y - 1)2 + (z + 2)2 = 66.
D. (x + 1)2 + (y + 1)2 + (z - 2)2 = 46.
Lời giải:
Đáp án : B
Giải thích :
Gọi H là chân đường vuông góc của I trên AB
Xét tam giác AHI vuông tại H, AI = R có:
IH=AI.sin(IABˆ) =R.sin(300)=R/2
Điểm M (-1; 3; 2) ∈d
⇒ IM→=(-2;2; 4)
Đường thẳng Δ có một vecto chỉ phương là u→=(1; 2;1)
Ta có: [IM→ ; u→ ]=(-6;6;-6)
⇒ d(I,Δ)
Ta có: IH = d(I,Δ)
⇒ R/2=3√2 ⇒ R=6√2
Vậy phương trình mặt cầu cần tìm là:
(x-1)2 +(y-1)2 +(z+2)2 =72
Bài 24: Phương trình mặt cầu có tâm I(3; √3; -7) và tiếp xúc trục tung là:
A. (x + 3)2 + (y + √3)2 + (z - 7)2 = 58.
B. (x - 3)2 + (y - √3)2 + (z + 7)2 = 61.
C. (x - 3)2 + (y - √3)2 + (z + 7)2 = 58.
D. (x - 3)2 + (y - √3)2 + (z + 7)2 = 12.
Lời giải:
Đáp án : C
Giải thích :
Khoảng cách từ điểm I đến trục Oy là
d= √(32 +72) =58
Do mặt cầu tiếp xúc với Oy nên R = d
Vậy phương trình mặt cầu cần tìm là
(x -3)2 +(y -√3)2 +(z+7)2 =72
Bài 25: Phương trình mặt cầu có tâm I(√5; 3; 9) và tiếp xúc trục hoành là:
A. (x - √5)2 + (y - 3)2 + (z - 9)2 = 90.
B. (x - √5)2 + (y - 3)2 + (z - 9)^} = 14.
C. (x + √5)2 + (y + 3)2 + (z + 9)2 = 86.
D. (x + √5)2 + (y + 3)2 + (z + 9)2 = 90.
Lời giải:
Đáp án : A
Giải thích :
Khoảng cách từ điểm I đến trục Ox là
d=√(32 +92)=90
Do mặt cầu tiếp xúc với Ox nên R = d
Vậy phương trình mặt cầu cần tìm là
(x -√5)2 +(y-3)2 +(z-9)2 =72
Bài 26: Phương trình mặt cầu có tâm I(-√6; -√3; √2 -1) và tiếp xúc trục Oz là:
A. (x + √6)2 + (y + √3)2 + (z - √2 + 1)2 = 3.
B. (x + √6)2 + (y + √3)2 + (z - √2 - 1)2 = 9.
C. (x + √6)2 + (y + √3)2 + (z - √2 - 1)2 = 3.
D. (x + √6)2 + (y + √3)2 + (z - √2 + 1)2 = 9.
Lời giải:
Đáp án : D
Giải thích :
Khoảng cách từ I đến trục Oz là
d=√(6+3)=9
Do mặt cầu tiếp xúc với Ox nên R = d
Vậy phương trình mặt cầu cần tìm là
(x -√6)2 +(y-√3)2 +(z-√2+1)2 =9
Bài 27: Phương trình mặt cầu có tâm I(4;6;-1) và cắt trục Ox tại hai điểm A, B sao cho tam giác IAB vuông là:
A. (x - 4)2 + (y - 6)2 + (z + 1)2 = 26.
B. (x - 4)2 + (y - 6)2 + (z + 1)2 = 74.
C. (x - 4)2 + (y - 6)2 + (z + 1)2 = 34.
D. (x - 4)2 + (y - 6)2 + (z + 1)2 = 104.
Lời giải:
Đáp án : B
Giải thích :
Khoảng cách từ I đến trục Ox là:
h =√(62 +1)=√37
Vì tam giác IAB cân tại I nên tam giác IAB vuông cân tại I
Gọi R là bán kính mặt cầu ⇒ IA=IB=R;AB=R√2
Ta có: IA . IB = h . AB ⇒ R2 =√37 . R√2 ⇒ R=√74
Vậy phương trình mặt cầu cần tìm là
(x-4)2 +(y-6)2 +(z+1)2 =74
Bài 28: Phương trình mặt cầu có tâm I(3;6;-4) và cắt trục Oz tại hai điểm A, B sao cho diện tích tam giác IAB bằng 6√5 là:
A. (x - 3)2 + (y - 6)2 + (z + 4)2 = 49.
B. (x - 3)2 + (y - 6)2 + (z + 4)2 = 45.
C. (x - 3)2 + (y - 6)2 + (z + 4)2 = 36.
D. (x - 3)2 + (y - 6)2 + (z + 4)2 = 54.
Lời giải:
Đáp án : A
Giải thích :
Khoảng cách từ điểm I đến trục Oz là:
h=√(32 +62)= 3√5
Ta có:
SIAB=1/2 h . AB ⇒ AB=(2SIAB)/h =4
Gọi R là bán kính mặt cầu
⇒ R2 =h2 +(AB/2)2 =49
Phương trình mặt cầu cần tìm là:
(x-3)2 +(y-6)2 +(z+4)2 =49
Bài 29: Cho các điểm I(-1;0;0) và đường thẳng 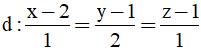. Phương trình mặt cầu (S) có tâm I và tiếp xúc d là:
A. (x + 1)2 + y2 + z2 = 10.
B. (x - 1)2 + y2 + z2 = 5.
C. (x + 1)2 + y2 + z2 = 5.
D. (x - 1)2 + y2 + z2 = 10.
Lời giải:
Đáp án : C
Giải thích :
Đường thẳng d đi qua điểm M (2; 1; 1) và có vecto chỉ phương u→=(1;2;1)
IM→=(3;1;1) ⇒ [IM→ , u→ ]=(-1; -2;5)
Khoảng cách từ điểm I đến đường thẳng d là:
d(I,d)
Do mặt cầu tiếp xúc với d nên d(I,d)=R
Vậy phương trình mặt cầu cần tìm là:
(x+1)2 +y2 +z2 =5
Bài 30: Cho các điểm A(1;3;1) và B(3;2;2). Mặt cầu đi qua hai điểm A, B và tâm thuộc trục Oz có đường kính là:
A. 2√6 B. √(14)
C. 2√(10) D. 2√(14)
Lời giải:
Đáp án : D
Giải thích :
Gọi I là tâm của mặt cầu, do I thuộc trục Oz nên I (0; 0; c)
Mặt cầu đi qua 2 điểm A, B nên IA = IB = R
⇒ IA2 =IB2
⇔ 12 +32 +(c-1)2 =32 +22 +(c-2)2
⇔ 2c=6 ⇔ c=3
Vậy I (0; 0; 3); R= IA = √14
⇒ Đường kính của mặt cầu là 2√14
Bài 31: Cho các điểm A(0;1;3), B(2;2;1) và đường thẳng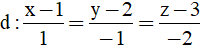 
. Mặt cầu đi qua hai điểm A, B và tâm thuộc đường thẳng d thì tọa độ tâm là:
A. (3/2; 3/2; 2) B. (13/10; 17/10; 12/5)
C. (4/3; 2/3; 7/3) D. (6/5; 9/5; 13/5)
Lời giải:
Đáp án : B
Giải thích :
Phương trình tham số của đường thẳng d:
Gọi I là tâm mặt cầu, do I thuộc đường thẳng d nên I(1+t;2-t;3-2t)
Mặt cầu đi qua 2 điểm A, B nên IA = IB = R
⇒ IA2 =IB2
⇔ (1+t)2 +(1-t)2 +4t2 =(t-1)2 +t2 +(2-2t)2
⇔ t=(-3)/10
⇒ I(17/10; 17/10; 12/5)
Bài 32: Cho các điểm A(-2;4;1), B(2;0;3) và đường thẳng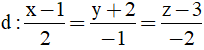 
. Gọi (S) là mặt cầu đi qua A, B và có tâm thuộc đường thẳng d. Bán kính mặt cầu (S) bằng:
A. (√1169)/4 B. (√873)/4
C. 1169/16 D. (√967)/2
Lời giải:
Đáp án : A
Giải thích :
Phương trình tham số của đường thẳng d là: 
Gọi I là tâm của mặt cầu, do I thuộc d nên I (1+2t; -2-t; 3-2t)
Mặt khác mặt cầu đi qua A, B nên IA = IB = R
⇒ IA2 =IB2
⇔ (2t+3)2 +(t+6)2 +(2-2t)2 =(2t-1)2 +(t+2)2 +4t2
⇔ t=(-11)/4
⇒ R=IA= √(1169)/4
Bài 33: Mặt cầu tâm I(2;4;6) và tiếp xúc với mặt phẳng (Oxy) có phương trình:
A. (x - 2)2 + (y - 4)2 + (z - 6)2 = 36.
B. (x - 2)2 + (y - 4)2 + (z - 6)2 = 16.
C. (x - 2)2 + (y - 4)2 + (z - 6)2 = 4.
D. (x - 2)2 + (y - 4)2 + (z - 6)2 = 56.
Lời giải:
Đáp án : A
Giải thích :
Chú ý:
Khoảng cách từ điểm I (a; b; c) đến mặt phẳng (Oxy) là: d=|c|
Khoảng cách từ điểm I (a; b; c) đến mặt phẳng (Oyz) là: d=|a|
Khoảng cách từ điểm I (a; b; c) đến mặt phẳng (Oxz) là: d=|b|
Khoảng cách từ điểm I (2; 4; 6) đến mặt phẳng Oxy là d = 6
Khi đó, mặt cầu tâm I(2; 4; 6) và tiếp xúc với mặt phẳng Oxy là:
(x-2)2 +(y-4)2 +(z-6)2 =36
Bài 34: Mặt cầu tâm I(2;4;6) và tiếp xúc với mặt phẳng (Oxz) có phương trình:
A. (x - 2)2 + (y - 4)2 + (z - 6)2 = 36.
B. (x - 2)2 + (y - 4)2 + (z - 6)2 = 4.
C. (x - 2)2 + (y - 4)2 + (z - 6)2 = 16.
D. (x - 2)2 + (y - 4)2 + (z - 6)2 = 56.
Lời giải:
Đáp án : B
Bài 35: Trong không gian Oxyz, mặt cầu có đường kính AB với A(4; -3;7), B(2;1;3) là:
A. (x + 3)2 + (y - 1)2 + (z + 5)2 = 9
B. (x - 3)2 + (y + 1)2 + (z - 5)2 = 9
C. (x + 3)2 + (y - 1)2 + (z + 5)2 = 3
D. (x - 3)2 + (y + 1)2 + (z - 5)2 = 3
Lời giải:
Đáp án : B
Giải thích :
Mặt cầu có đường kính AB nên trung điểm I của AB là tâm mặt cầu và
R= IA= AB/2
⇒ I(3; -1;5); R=AB/2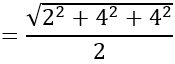
=3
Vậy pt mặt cầu cần tìm là:
(x-3)2 +(y+1)2 +(z-5)2 =9
Bài 36: Trong không gian Oxyz, mặt cầu tâm I(1;2;4) tiếp xúc với mặt phẳng (α): 2x + 2y + z - 1 = 0 có phương trình là :
A. (x + 1)2 + (y + 2)2 + (z + 4)2 = 1
B. (x - 4)2 + (y - 2)2 + (z - 1)2 = 1
C. (x - 1)2 + (y - 2)2 + (z - 4)2 = 9
D. (x - 1)2 + (y - 2)2 + (z - 4)2 = 3
Lời giải:
Đáp án : C
Giải thích :
Khoảng cách từ tâm I đến mặt phẳng (α) là :
d(I; (α))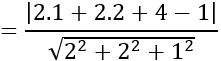
=3
Do mặt cầu tiếp xúc với mặt phẳng nên khoảng cách từ I đến mặt phẳng bằng R
Vậy phương trình mặt cầu là :
(x-1)2 +(y-2)2 +(z-4)2 =9
Bài 37: Trong không gian Oxyz, mặt cầu tâm I(1;1;2) và đi qua A(-2; 1; 6) có phương trình là :
A. (x + 1)2 + (y + 1)2 + (z + 2)2 = 25
B. (x - 1)2 + (y - 1)2 + (z - 2)2 = 5
C. (x + 1)2 + (y + 1)2 + (z + 2)2 = 5
D. (x - 1)2 + (y - 1)2 + (z - 2)2 = 25
Lời giải:
Đáp án : D
Giải thích :
Gọi R là bán kính mặt cầu
⇒ R =IA = √(32 +42)=5
Vậy phương trình mặt cầu cần tìm là :
(x-1)2 +(y-1)2 +(z-2)2 =25
Bài 38: Trong không gian Oxyz, mặt cầu đi qua bốn điểm A(6; -2; 3), B(0; 1; 6), C(2; 0; -1) và D(4; 1; 0) có phương trình là:
A. x2 + y2 + z2 - 4x + 2y - 6z - 3 = 0
B. 2x2 + y2 + z2 - 4x + 2y - 6z - 3 = 0
C. x2 + y2 + z2 + 4x - 2y + 6z - 3 = 0
D. x2 + y2 + z2 - 4x + 2y - 6z + 3 = 0
Lời giải:
Đáp án : A
Giải thích :
Gọi I (x; y; z) là tâm của mặt cầu
Do mặt cầu ngoại tiếp tứ diện ABCD nên ta có IA = IB = IC = ID
Khi đó: R2 =IA2 =17
Phương trình mặt cầu cần tìm là:
(x-2)2 +(y+1)2 +(z-3)2 =17
⇔ x2 +y2 +z2 -4x +2y -6z -3 =0
Bài 39: Trong không gian Oxyz, cho bốn điểm A(1;1;0), B(0;1;0), C(0;0;1) và O(0;0;0). Khi đó mặt cầu ngoại tiếp tứ diện OABC có phương trình là :
A. x2 + y2 + z2 + x + y + z = 0
B. x2 + y2 + z2 - 2x - 2y - 2z = 0
C. x2 + y2 + z2 - x - y - z = 0
D. x2 + y2 + z2 + 2x + 2y + 2z = 0
Lời giải:
Đáp án : C
Giải thích :
Gọi Phương trình mặt cầu cần tìm là
x2 +y2 +z2 -2ax -2by -2cz +d =0
Ta có : O(O;0;0)∈(S) ⇒ d=0
A(1;0;0)∈(S) ⇒ 1-2a+d=0
B(0;1;0)∈(S) ⇒ 1-2b+d=0
C(0;1;0)∈(S) ⇒ 1-2c+d=0
⇒ a=b=c=1/2
Vậy phương trình mặt cầu cần tìm là :
x2 +y2 +z2 -x -y -z =0
Bài 40: Trong không gian Oxyz, phương trình mặt cầu (S) qua ba điểm A(1; -2; 4), B(1; 3; -1), C(2; -2; -3) và có tâm nằm trên mặt phẳng Oxy là :
A. x2 + y2 + z2 + 4x + 2y + 21 = 0
B. x2 + y2 + z2 + 4x + 2y + 3z - 21 = 0
C. x2 + y2 + z2 - 4x + 2y - 21 = 0
D. x2 + y2 + z2 + 4x + 2y - 21 = 0
Lời giải:
Đáp án : D
Giải thích :
Gọi I là tâm mặt cầu, do I nằm trên mặt phẳng (Oxy) nên I (a; b; 0)
Do mặt cầu đi qua 3 điểm A, B, C nên IA = IB = IC = R
Vậy I (-2 ; -1 ; 0); R=IA=√26
Phương trình mặt cầu cần tìm là:
(x+2)2 +(y+1)2 +z2 =26
⇔ x2 +y2 +z2 +4x +2y -21 =0
Bài 41: Trong không gian Oxyz, cho hai điểm A(1;2;0), B(-3;4;2) và I là điểm thuộc trục Ox. Phương trình mặt cầu tâm I qua A, B có phương trình là:
A. (x - 3)2 + y2 + z2 = 20
B. (x + 3)2 + y2 + z2 = 20
C. (x + 1)2 + (y - 3)2 + (z - 1)2 = 11/4
D. (x + 1)2 + (y - 3)2 + (z - 1)2 = 20
Lời giải:
Đáp án : B
Giải thích :
I thuộc trục Ox nên I (a; 0; 0)
Mặt cầu đi qua A, B nên IA = IB = R
⇒ IA2=IB2
⇔ (a-1)2 +22 =(a+3)2 +42 +22
⇔ a= -3
⇒ I(-3;0;0); R= IA= √20
Phương trình mặt cầu là:
(x+3)2 +y2 +z2 =20
Bài 42: Trong không gian với hệ trục Oxyz, cho điểm A(-3;1;2) điểm B(1;-1;0) phương trình mặt cầu nhận AB làm đường kính có tọa độ tâm là:
A. (-2;0;2) B. (-1;0;1)
C. (1;0;1) D. (1;0;-1)
Lời giải:
Đáp án : B
Giải thích :
AB là đường kính mặt cầu nên trung điểm I của AB là tâm của mặt cầu
⇒ I(-1;0;1)
Bài 43: Trong không gian với hệ trục Oxyz, cho điểm A(5;1;0) và điểm I(1;2;3) mặt cầu tâm I đi qua A có phương trình là.
A. (x - 1)2 + (y - 2)2 + (z - 3)2 = 26
B. (x - 1)2 + (y - 2)2 + (z - 3)2 = √26
C. (x + 1)2 + (y - 2)2 + (z - 3)2 = 26
D. (x - 1)2 + (y - 2)2 + (z + 3)2 = √26
Lời giải:
Đáp án : C
Giải thích :
Do mặt cầu đi qua A nên IA = R
IA= √(42 +12 +32)=26
Phương trình mặt cầu cần tìm là:
(x-1)2 +(y-2)2 +(z-3)2=26
Bài 44: Trong không gian Oxyz, mặt cầu tâm I(1;2;-3) tiếp xúc mặt phẳng (P): 2x+2y-z-3=0 có pt là :
A. (x + 1)2 + (y - 2)2 + (z - 3)2 = 4
B. (x - 1)2 + (y - 2)2 + (z + 3)2 = 4
C. (x - 1)2 + (y - 2)2 + (z - 3)2 = 16
D. (x - 1)2 + (y - 2)2 + (z + 3)2 = 2
Lời giải:
Đáp án : B
Giải thích :
Khoảng cách từ tâm I(1; 2; -3) đến mặt phẳng (P) là:
d(I;(P))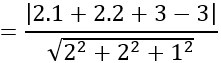
=2
Phương trình mặt cầu cần tìm là:
(x-1)2 +(y-2)2 +(z+3)2 =4
Bài 45: Trong không gian Oxyz, mp (P): √(3)x – y + 6 = 0 cắt mc (S) tâm O theo giao tuyến là một đường tròn có bán kính r = 4. PT mặt cầu (S) là :
A. x2 + y2 + z2 = 25
B. x2 + y2 + z2 = 5
C. x2 + y2 + z2 = 1
D. x2 + y2 + z2 = 7
Lời giải:
Đáp án : A
Giải thích :
Khoảng cách từ O đến mặt phẳng (P) là:
d=d(I;(P))=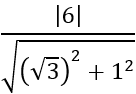
=3
Gọi R là bán kính của mặt cầu
⇒ R2 =r2 +d2 =42 +32 =25
Vậy phương trình mặt cầu cần tìm là:
x2 +y2 +z2 =25
Bài 46: Cho mặt cầu (S); x2 + y2 + z2 – 2x – 2y + 2z – 1 = 0. chọn phát biểu đúng :
A. (S) có tâm I(-1;-1;1)
B. (S) có bán kính bằng 4
C. điểm A(1;1;-3) thuộc (S)
D. điểm B(-1;-1;-3) thuộc (S)
Lời giải:
Đáp án : C
Giải thích :
(S): x2 +y2 +z2 -2x -2y +2z -1 =0
Mặt cầu (S) có tâm (1; 1; -1) ; R = √(a2 +b2 +c2 -d)=2
Thay tọa độ điểm A, B vào phương trình mặt cầu (S) thì tọa độ điểm A thỏa mãn
Vậy đáp án đúng là C
Bài 47: Trong không gian với hệ toạ độ Oxyz, cho tứ diện ABCD có toạ độ các đỉnh là A(1;1;1) , B(1;2;1) , C(1;1;2) , D(2;2;1) Viết phương trình mặt cầu (S) ngoại tiếp tứ diện ABCD.
A. x2 + y2 + z2 - 3x - 3y - 3z - 6 = 0
B. x2 + y2 + z2 - 3x - 3y - 3z + 6 = 0
C. x2 + y2 + z2 - 3x + 3y - 3z + 6 = 0
D. x2 + y2 + z2 - 3x - 3y - 3z + 12 = 0
Lời giải:
Đáp án : B
Giải thích :
Gọi I (a; b; c) là tâm mặt cầu
Mặt cầu ngoại tiếp tứ diện ABCD nên ta có IA = IB = IC = ID = R.
⇒ R=IA= √3/2
Phương trình mặt cầu ngoại tiếp tứ diện ABCD là:
(x-3/2)2 +(y-3/2)2 +(z-3/2)2 =3/4
⇔ x2 +y2 +z2 -3x -3y -3z +6 =0
Bài 48: Trong không gian Oxyz, cho mặt phẳng (P): 2x + y - 2z + 10 = 0 và điểm I(2;1;3). Phương trình mặt cầu (S) tâm I cắt mặt phẳng (P)theo một đường tròn (C)có bán kính bằng 4 là
A. (x + 2)2 + (y + 1)2 + (z + 3)2 = 25
B. (x - 2)2 + (y - 1)2 + (z - 3)2 = 7
C. (x + 2)2 + (y - 1)2 + ( z - 3)2 = 9
D. (x - 2)2 + (y - 1)2 + (z - 3)2 = 25
Lời giải:
Đáp án : D
Giải thích :
Khoảng cách từ điểm I đến mặt phẳng (P) là:
d=d(I;(P))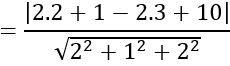
=3
Gọi R là bán kính mặt cầu
Ta có: R2 =d2 +r2 =32 +42 =25
Vậy phương trình mặt cầu cần tìm là:
(x-2)2 +(y-1)2 +(z-3)2 =25
Bài 49: Trong không gian hệ tọa độ Oxyz cho 2 đường thẳng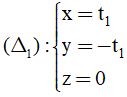 
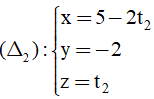
t1 ∈ R và
t2 ∈ R. Lập phương trình mặt cầu (S) có tâm I∈(Δ1) và I cách (Δ2) một khoảng bằng 3. Cho biết mặt phẳng (α): 2x + 2y – 7z = 0 cắt mặt cầu (S) theo một đường tròn giao tuyến có bán kính r = 5 .
A. (S1): x2 +y2 +z2 =25
(S2 ): (x-5)2 +(y+5)2 +z2 =25
B. (S1 ): x2 +y2 +z2 =16
(S2): (x+5)2 +(y-5)2 +z2 =16
C. (S1 ): (x-1)2 +(y+1)2 +z2 =25;
(S2 ): (x-5)2 +(y+5)2 +z2 =25
D. (S1 ): (x-1)2 +(y+1)2 +z2 =16;
(S2 ): (x-5)2 +(y+5)2 +z2 =16
Lời giải:
Đáp án : A
Giải thích :
Tâm I thuộc Δ1 nên I (t; -t; 0)
Điểm M (5; -2; 0) thuộc Δ2 và một vecto chỉ phương là u→=(-2;0;1)
IM→=(5-t; -2+t; 0)
⇒ [IM→ ; u→ ]=(t-2; t-5; 2t-4)
Khi đó, khoảng cách từ I đến Δ2 là:
d(I; Δ2 )
=3 ⇔ 6t2 -30t +45 =45
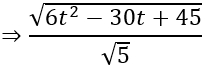
+ Điểm I1 (0;0;0) thuộc mặt phẳng (P) nên bán kính của đường tròn giao tuyến là bán kính của mặt cầu.
Phương trình mặt cầu là:
x2 +y2 +z2 =25
+ Điểm I2 (5; -5;0) thuộc mặt phẳng (P) nên bán kính của đường tròn giao tuyến là bán kính của mặt cầu.
Phương trình mặt cầu là:
(x-5)2 +(y+5)2 +z2 =25
Bài 50: Trong không gian với hệ tọa độ Oxyz : Cho đường thẳng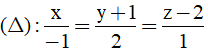 
và (P): 2x – y – 2z – 3 = 0. Viết phương trình mặt cầu (S) có tâm I thuộc (Δ); I cách (P) một khoảng bằng 2 và (P) cắt mặt cầu (S) một đường tròn giao tuyến (C) có bán kính bằng 3.
A. (S1 ): x2 +(y-1)2 +(z+2)2 =13
(S2 ): (x+2)2 +(y-5)2 +z2 =13
B. (S1 ): x2 +(y+1)2 +(z-2)2 =13
(S2 ): (x-2)2 +(y+5)2 +z2 =13
C. (S1 ): (x-1)2 +(y-3)2 +(z-2)2 =13
(S2): (x+3)2 +(y-5)2 +(z-3)2 =13
D. (S1 ): (x-1)2 +(y-3)2 +(z-2)2 =13
(S2 ): (x+3)2 +(y-5)2 +(z-3)2 =13
Lời giải:
Đáp án : B
Giải thích :
Phương trình tham số của đường thẳng
Do I thuộc đường thẳng Δ nên I(-t; -1+2t;2+t)
Khoảng cách từ I đến mặt phẳng (P) là:
d(I;(P))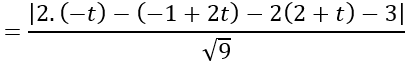
=|2t+2|
Theo đề bài: d(I;(P))=2
⇒ |2t+2|=2 ⇔ |t+1|=1 ⇔ 
Với t = 0, ta có I (0; -1; 2)
Với t = -2, ta có I (2; -5; 0)
Gọi R là bán kính của mặt cầu
⇒ R2 =r2 +d2 =32 +22 =13
Vậy có 2 phương trình mặt cầu thỏa mãn đề bài là:
(S1 ): x2 +(y+1)2 +(z-2)2 =13
(S2 ): (x-2)2 +(y+5)2 +z2 =13
Bài 51: Phương trình của mặt cầu đi qua ba điểm A(1;2;-4), B(1;-3;1), C(2;2;3) và có tâm nằm trên mặt phẳng tọa độ Oxy là :
A. x2 + y2 + z2 + 4x - 2y - 21 = 0
B. x2 + y2 + z2 + 4x - 2y + 21 = 0
C. x2 + y2 + z2 - 4x + 2y - 21 = 0
D. x2 + y2 + z2 - 4x + 2y + 21 = 0
Lời giải:
Đáp án :
Giải thích :A
Bài 51: Chọn A
Do tâm I của mặt cầu thuộc mặt phẳng tọa độ Oxy nên I (a; b; 0)
Lại có mặt cầu đi qua 3 điểm A, B, C nên IA = IB = IC = R
Vậy I (-2 ; 1 ; 0), R=IA= √26
Phương trình mặt cầu cần tìm là :
(x+2)2 +(y-1)2 +z2 =26
⇔ x2 +y2 +z2 + 4x -2y -21 =0
Bài 52: Viết phương trình của mặt cầu (S) biết (S) có tâm I(3;-2;0) và (S) cắt trục Oy tại hai điểm A,B mà AB=8:
A. (x - 3)2 +(y + 2)2 +z2 = 9
B. (x - 3)2 +(y + 2)2 +z2 = 64
C. (x + 3)2 +(y - 2)2 +z2 = 25
D. (x - 3)2 +(y + 2)2 +z2 = 25
Lời giải:
Đáp án : D
Giải thích :
Khoảng cách từ I đến trục Oy là : d= √(32 +0)=3
Gọi R là bán kính mặt cầu
⇒ R2 =d2 +(AB/2)2 =32 +42 =25
Phương trình mặt cầu cần tìm là :
(x-3)2 +(y+2)2 +z2 =25
Bài 53: Biết mặt cầu (S) có tâm tâm I(-1; -4; 3) và (S) cắt mặt phẳng tọa độ Oxz theo một đường tròn có diện tích bằng 9π. Khi đó phương trình của (S) là:
A. (x - 1)2 + (y - 4)2 + (z + 3)2 = 16
B. (x + 1)2 + (y + 4)2 + (z - 3)2 = 9
C. (x - 1)2 + (y - 4)2 + (z + 3)2 = 25
D. (x + 1)2 + (y + 4)2 + (z - 3)2 = 25
Lời giải:
Đáp án : C
Giải thích :
Khoảng cách từ I đến mặt phẳng (Oxz) là d = 4
Mặt phẳng (Oxz) cắt mặt cầu theo một đường tròn có diện tích bằng 9π
⇒ S=πr2 =9π ⇒ r=3
Gọi R là bán kính mặt cầu
⇒ R2 =r2 +d2 =32 +42 =25
Vậy phương trình mặt cầu cần tìm là :
(x+1)2 +(y+4)2 +(z-3)2 =25
Bài 54: Viết phương trình của mặt cầu (S) biết (S) tiếp xúc với mặt phẳng tọa độ Oxz tại điểm M(-2; 0; 1) và (S) đi qua điểm A(2;2;1)
A. (x - 2)2 + (y - 2)2 + (z - 1)2 = 20
B. (x + 2)2 +y2 + (z - 1)2 = 20
C. (x + 2)2 + (y - 5)2 + (z - 1)2 = 25
D. (x + 2)2 + (y - 5)2 + (z - 1)2 = 20
Lời giải:
Đáp án : C
Giải thích :
Gọi I (a; b; c) là tọa độ tâm của mặt cầu.
⇒ IM→=(-2-a; -b; 1-c)
Mặt phẳng (Oxz) có vecto pháp tuyến n→=(0 ;1 ;0)
Do mặt cầu (S) tiếp xúc với mặt phẳng tọa độ (Oxz) tại M nên
Giải (1) :
IM→=k n→
Do mặt cầu đi qua A(2; 2;1) nên IA = R
Ta có : IA2 =42 +(k+2)2 =k2 +4k+20
Từ (2) ⇒ IA2 =R2 =k2 ⇒ k2 +4k +20 =k2
⇒ k= -5
Vậy I (-2 ; 5 ; 1) và R = 5
Phương trình mặt cầu cần tìm là :
⇒ (x+2)2 +(y-5)2 + (z-1)2 =25
Bài 55: Trong không gian với hệ tọa độ Oxyz, cho đường thẳng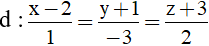
và mặt phẳng (P): x+2y + z + 9 = 0. Phương trình mặt cầu tiếp xúc với mặt phẳng (P) có tâm thuộc đường thẳng d và có bán kính R = √(3/2) là:
A. (x-5)2 +(y+10)2 +(z-3)2= 3/2
B. x2 + ( y - 1)2 + ( z + 1)2 = 4
C. x2 + ( y + 1)2 + ( z - 1)2 = 9
D. (x+5)2 + (y-10)2 + (z+3)2 = 3/2
Lời giải:
Đáp án : A
Giải thích :
Phương trình tham số của đường thẳng 
Do tâm I thuộc đường thẳng d nên I(2+t; -1-3t; -3+2t)
Khoảng cách từ điểm I đến mặt phẳng (P) là:
d(I;(P))
Mặt cầu tiếp xúc với mặt phẳng (P) nên d(I;(P))=R
⇔ |-t+2|=1 ⇔ 
Với t = 1 thì I (3; -4; -1)
Với t = 3 thì I (5; -10; 3)
Vậy có 2 phương trình mặt cầu thỏa mãn là:
(x-3)2 +(y+4)2 +(z+1)2 =3/2
(x-5)2 +(y+10)2 +(z-3)2 =3/2
Bài 56: Trong không gian với hệ tọa độ Oxyz , cho ba điểm A(1;0;0), B(0;3;0), C(0;0;6). Tìm phương trình mặt cầu (S) tiếp xúc với Oy tại B, tiếp xúc với Oz tại C và đi qua A ?
A. (x - 5)2 + (y - 3)2 + (z - 6)2 = 61
B. (x - 5)2 + (y + 3)2 + (z - 6)2 = 61
C. (x + 5)2 + (y - 3)2 + (z - 6)2 = 61
D. (x - 5)2 + (y - 3)2 + (z + 6)2 = 61
Lời giải:
Đáp án : A
Giải thích :
Gọi I (a; b; c) là tâm mặt cầu
IB→=(-a;3-b; -c); IC→=(-a; -b; 6-c)
Do mặt cầu (S) tiếp xúc với Oy tại B, tiếp xúc với Oz tại C nên
⇒ I(a;3;6)
I đi qua A nên ta có IA = IB
⇔ IA2 =IB2 ⇔ (a-1)2 +32 +62 =a2 +62
⇔ a=5
Khi đó, I (5; 3; 6) và R2 =IA2 =61
Vậy phương trình mặt cầu cần tìm là :
(x-5)2 +(y-3)2 +(z-6)2 =61
Bài 57: Cho điểm A(1;2;4) và mặt phẳng (P): x + y + z + 1 = 0. Phương trình mặt cầu (S) có tâm A, biết mặt cầu (S) cắt mặt phẳng (P) theo thiết diện là một đường tròn có chu vi 4π là:
A. (x + 1)2 + (y + 2)2 + (z + 4)2 = 76/3
B. (x - 1)2 + (y - 2)2 + (z - 4)2 = 9
C. (x + 1)2 + (y + 2)2 + (z + 4)2 = 9
D. (x - 1)2 + (y - 2)2 + (z - 4)2 = 76/3
Lời giải:
Đáp án : D
Giải thích :
Khoảng cách từ A đến mặt phẳng (P) là:
Gọi r là bán kính của đường tròn thiết diện
Ta có: Chu vi của đường tròn là 2πr=4π ⇒ r=2
Gọi R là bán kính mặt cầu, ta có:
R2 =r2 +d2 =76/3
Phương trình mặt cầu cần tìm là:
(x-1)2 +(y-2)2 +(z-4)2 =76/3
Bài 58: Trong mặt phẳng Oxyz, Cho đường thẳng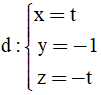 
và 2 mp (P): x + 2y + 2z + 3 = 0 và (Q): x + 2y + 2z + 7 = 0. Mặt cầu (S) có tâm I thuộc đường thẳng (d) và tiếp xúc với hai mặt phẳng (P) và (Q) có phương trình
A. (x + 3)2 +(y + 1)2 +(z - 3)2 = 4/9
B. (x - 3)2 +(y - 1)2 +(z + 3)2 = 4/9
C. (x + 3)2 +(y + 1)2 +(z + 3)2 = 4/9
D. (x - 3)2 +(y + 1)2 +(z + 3)2 = 4/9
Lời giải:
Đáp án : D
Giải thích :
Do I thuộc đường thẳng d nên I(t; -1; -t)
Ta có:
d(I;(P))
d(I;(Q))
Do mặt cầu tiếp xúc với 2 mặt phẳng nên d(I;(P))= d(I;(Q)) =R
⇔ t=3
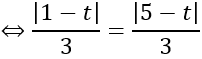
Với t = 3 thì I(3; -1; -3); R= 2/3
Vậy phương trình mặt cầu cần tìm là:
(x-3)2 +(y+1)2 +(z+3)2 =4/9
Bài 59: Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(1; -2; -4), B(2;3;4), C(3;5;7). Tìm phương trình mặt cầu có tâm là A và tiếp xúc với BC ?
A. (x+1)2 +(y-2)2 +(z-4)2 =5/2
B. (x-1)2 +(y+2)2 +(z+4)2 =5/2
C. (x+1)2 +(y-2)2 +(z-4)2 =25/4
D. (x-1)2 +(y+2)2 +(z+4)2 =25/4
Lời giải:
Đáp án : B
Giải thích :
Đường thẳng BC đi qua B (2; 3; 4) và có vecto chỉ phương BC→=(1;2;3)
AB→=(1;5;8); BC→=(1;2;3)
⇒ [AB→ , BC→ ]=(-1;5;-3)
Khoảng cách từ A đến BC là:
d(A;BC)
Phương trình mặt cầu cần tìm là:
(x-1)2 +(y+2)2 +(z+4)2 =5/2
Bài 60: Cho ba điểm A (6; -2; 3), B(0; 1; 6), C(2; 0; -1), D(4; 1; 0). Viết phương trình mặt cầu ngoại tiếp tứ diện ABCD
A. (x+2)2 +(y-1)2 +(z-3)2 =17
B. (x-2)2 +(y-1)2 +(z-3)2 =17
C. (x-2)2 +(y+1)2 +(z-3)2 =17
D. (x+2)2 +(y+1)2 +(z+3)2 =17
Lời giải:
Đáp án : C
Giải thích :
Gọi I (x; y; z) là tâm của mặt cầu
Do mặt cầu ngoại tiếp tứ diện ABCD nên ta có IA = IB = IC = ID
Khi đó: R2 =IA2 =17
Phương trình mặt cầu cần tìm là:
(x-2)2 +(y+1)2 +(z-3)2 =17
