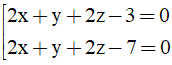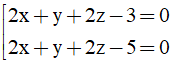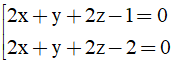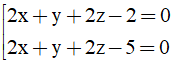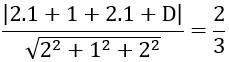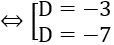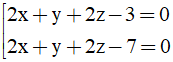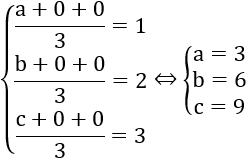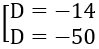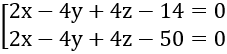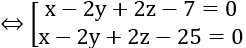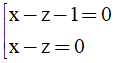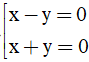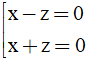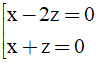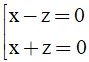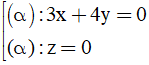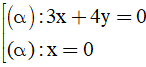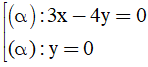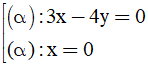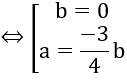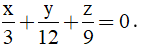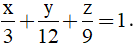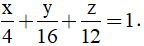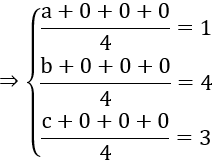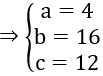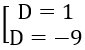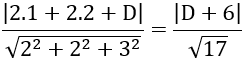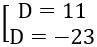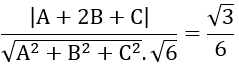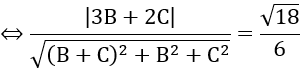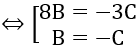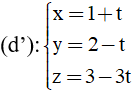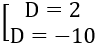50 bài tập trắc nghiệm Viết phương trình mặt phẳng chọn lọc, có đáp án - Toán lớp 12

---

50 bài tập trắc nghiệm Viết phương trình mặt phẳng chọn lọc, có đáp án

Với 50 bài tập trắc nghiệm Viết phương trình mặt phẳng chọn lọc, có đáp án Toán lớp 12 tổng hợp 50 bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Viết phương trình mặt phẳng từ đó đạt điểm cao trong bài thi môn Toán lớp 12.

Bài 1: Trong không gian Oxyz, Phương trình mặt phẳng (P) chứa trục Ox và vuông góc với mặt phẳng (Q): 3x + y - 2z - 5 = 0 là

   A. -x +3y =0

   B. 2x +3y =0

   C. 2y -z =0

   D. 2y +z =0

Lời giải:

Đáp án : D

Giải thích :

Trục Ox có vecto chỉ phương u→=(1;0;0) và đi qua điểm O (0; 0; 0)

Mặt phẳng (Q) có vecto pháp tuyến n_Q→=(3;1; -2)

Do mặt phẳng (P) chứa trục Ox và vuông góc với mặt phẳng (Q) nên mặt phẳng (P) có vecto pháp tuyến là n→=[u→ ; n_Q→ ]=(0;2;1)

Phương trình mặt phẳng (P) có vecto pháp tuyến n→ và đi qua điểm O là:

2y +z =0

Bài 2: Trong không gian Oxyz, cho điểm A(1;1;1) và mặt phẳng (Q): 2x + y + 2z - 1 = 0. Mặt phẳng (P) song song với mặt phẳng (Q) và khoảng cách từ A đến mặt phẳng (P) bằng 2/3. Phương trình mặt phẳng (P) là

   A.

   B.

   C.

   D.

Lời giải:

Đáp án : A

Giải thích :

Mặt phẳng (P) song song với mặt phẳng (Q) nên phương trình mặt phẳng (P) có dạng:

2x +y +2z +D =0 (D≠ -1)

Khoảng cách từ A đến mặt phẳng (P) bằng 2/3 nên ta có:

⇔ |5 +D| =2

Vậy phương trình mặt phẳng (P) cần tìm là:

Bài 3: Trong không gian Oxyz phương trình mặt phẳng (P) đi qua điểm A(2; -1; 2) song song trục Oy và vuông góc với mặt phẳng (Q): 2x - y + 3z - 9 = 0 là

   A. 3y + z + 1 = 0

   B. x + 2y = 0

   C. 3x - 2z - 2 = 0

   D. 3x + 2y - 10 = 0

Lời giải:

Đáp án : C

Giải thích :

Trục Oy có vecto chỉ phương là u→=(0;1;0)

Mặt phẳng (Q) có vecto pháp tuyến n_Q→=(2;-1;3)

Do mặt phẳng (P) chứa trục Ox và vuông góc với mặt phẳng (Q) nên mặt phẳng (P) có vecto pháp tuyến là n→=[u→ ; n_Q→ ]=(3;0; -2)

Phương trình mặt phẳng (P) có vecto pháp tuyến n→ và đi qua điểm A(2; -1; 2) là:

3(x -2) -2(z -2) =0

⇔ 3x -2z -2 =0

Bài 4: Phương trình mặt phẳng (α) đi qua M(1; -2; 3) và song song với mặt phẳng (β): 2x – 3y + z + 5 = 0 là :

   A. 2x – 3y +z -11 = 0

   B. –x – 2y +3z -11 = 0

   C. 2x – 3y +2z +11 = 0

   D. 2x – 3y +z +11 = 0

Lời giải:

Đáp án : A

Giải thích :

Mặt phẳng (α) song song với mặt phẳng (β): 2x – 3y + z + 5 = 0 nên phương trình mặt phẳng (α) có dạng: 2x -3y +z +D =0 (D≠5)

Mặt phẳng (α) đi qua M(1; -2; 3) nên:

2 .1 -3 .(-2) +3 +D =0 ⇒ D= -11

Vậy phương trình mặt phẳng cần tìm là 2x -3y +z -11 =0

Bài 5: Phương trình mặt phẳng (α) đi qua hai điểm A(3;1;-1), B(2;-1;4) và vuông góc với mặt phẳng có phương trình (β): 2x - y + 3z = 0 là :

   A. 2x - y+3z -2 = 0

   B. x -13y - 5z + 5 = 0

   C. - x +13y + 5z = 0

   D. x -13y - 5z +6 = 0

Lời giải:

Đáp án : B

Giải thích :

AB→ =(-1; -2;5)

Mặt phẳng (β) có vecto pháp tuyến n₁→=(2 ; -1 ;3)

Do mặt phẳng (α) đi qua hai điểm A, B và vuông góc với mặt phẳng (β) nên có vecto pháp tuyến là n→=[AB→ ; n₁→ ]=(-1;13;5)

Phương trình mặt phẳng (α) có vecto pháp tuyến n→ và đi qua điểm A(3 ; 1 ; -1) là :

-(x -3) +13(y -1) +5(z +1) =0

⇔ x -13y -5z +5 =0

Bài 6: Trong không gian với hệ toạ độ Oxyz, (α) là mặt phẳng đi qua điểm A(2; -1; 5) và vuông góc với hai mặt phẳng (P): 3x - 2y + z + 7 = 0 và (Q): 5x - 4y + 3z + 1 = 0. Phương trình mặt phẳng (α) là:

   A. x + 2y + z - 5 = 0

   B. 2x - 4y - 2z - 10 = 0

   C. 2x + 4y + 2z + 10 = 0

   D. x + 2y - z + 5 = 0

Lời giải:

Đáp án : A

Giải thích :

Mặt phẳng (P) có vecto pháp tuyến n₁→=(3; -2;1)

Mặt phẳng (Q) có vecto pháp tuyến n₂→=(5; -4;3)

Do mặt phẳng (α) vuông góc với 2 mặt phẳng (P) và (Q) nên vecto pháp tuyến của mặt phẳng (α) là n→=[n₁→ , n₂→ ]=(-2; -4; -2)= -2(1;2;1)

Phương trình mặt phẳng (α) đi qua A (2; -1; 5) và có vecto pháp tuyến n→=(1;2;1) là: x -2 +2(y +1) +z -5 =0

⇔ x +2y +z -5 =0

Bài 7: Trong không gian với hệ toạ độ Oxyz, gọi (α) là mặt phẳng qua G(1;2;3) và cắt các trục Ox, Oy, Oz lần lượt tại các điểm A, B, C (khác gốc O) sao cho G là trọng tâm của tam giác ABC. Khi đó mặt phẳng (α) có phương trình:

   A. 6x + 3y + 2z - 18 = 0

   B. 3x + 6y + 2z + 18 = 0

   C. 2x + y + 3z - 9 = 0

   D. 6x + 3y + 2z + 9 = 0

Lời giải:

Đáp án : A

Giải thích :

Giả sử tọa độ của các điểm là A (a; 0; 0), B (0; b; 0), C (0; 0; c)

Do G(1; 2; 3) là trọng tâm tam giác ABC nên ta có:

Mặt phẳng (α) đi qua A (3; 0; 0), B (0; 6; 0), C (0; 0; 9) có phương trình là:

x/3 +y/6 +z/9 =1

⇔ 6x +3y +2z -18 =0

Bài 8: Trong không gian với hệ toạ độ Oxyz, gọi (α) là mặt phẳng song song với mặt phẳng (β): 2x - 4y + 4z + 3 = 0 và cách điểm A(2; -3; 4) một khoảng k=3. Phương trình của mặt phẳng (α) là:

   A. x - 2y + 2z - 25 = 0 hoặc x - 2y + 2z - 7 = 0

   B. x - 2y + 2z - 25 = 0

   C. x - 2y + 2z - 7 = 0

   D. 2x - 4y + 4z - 5 = 0 hoặc 2x - 4y + 4z - 13 = 0

Lời giải:

Đáp án : A

Giải thích :

Phương trình mặt phẳng song song với mặt phẳng là:

2x -4y +4z +D =0 (D≠ 3)

Do cách điểm A( 2; -3; 4) một khoảng k = 3 nên ta có:

=3

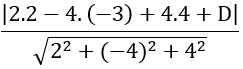
⇔ |32 +D| =18 ⇔

Vậy phương trình mặt phẳng là:

Bài 9: Trong không gian với hệ toạ độ Oxyz, cho A(1;0;0), B(0; b; 0), C(0; 0; c) (b > 0, c > 0) và mặt phẳng (P): y - z + 1 = 0. Viết phương trình mặt phẳng (ABC) biết mặt phẳng (ABC) vuông góc với mặt phẳng (P) và khoảng cách từ O đến (ABC) bằng 1/3 .

   A. x + 2y + z - 12 = 0

   B. x + 2y + 2z - 1 = 0

   C. 5x + 4y + 3z - 50 = 0

   D. x - y + z = 0

Lời giải:

Đáp án : B

Giải thích :

Phương trình mặt phẳng (ABC) đi qua A(1;0;0), B(0; b; 0), C(0; 0; c) (b > 0, c > 0) là:

x/1 +y/b +z/c =1 ⇔ bcx +cy +bz -bc =0

Mặt phẳng (ABC) có vecto pháp tuyến n→=(bc; c; b)

Mặt phẳng (P) có vecto pháp tuyến n₁→=(0;1; -1)

Do mặt phẳng (ABC) vuông góc với mặt phẳng (P) nên n→ .n₁→=0

⇔ c -b =0 ⇔ b =c

Khi đó phương trình mặt phẳng (ABC) là: b² x +by +bz -b² =0

⇔ bx +y +z -b =0

Khoảng cách từ O đến (ABC) bằng nên:

=1/3 ⇔ 9b² =b² +2 ⇔ b = 1/2 (do b > 0)

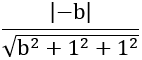
Vậy phương trình mặt phẳng (ABC) là

1/2 x +y +z -1/2 =0 ⇔ x +2y +2z -1 =0

Bài 10: Trong không gian với hệ toạ độ Oxyz, mặt phẳng (α) đi qua điểm M(5;4;3) và cắt các tia Ox, Oy, Oz các đoạn bằng nhau có phương trình là:

   A. x + y + z - 12 = 0

   B. x + y + z = 0

   C. 5x + 4y + 3z - 50 = 0

   D. x - y + z = 0

Lời giải:

Đáp án : A

Giải thích :

Do mặt phẳng (α) cắt các tia Ox, Oy, Oz các đoạn bằng nhau nên mặt phẳng (α) có phương trình:

x/a +y/a +z/a =1

Mặt khác, mặt phẳng (α) đi qua M (5; 4; 3) nên ta có:

5/a +4/a +3/a =1 ⇔ a=12

Vậy phương trình mặt phẳng (α) là:

x/12 +y/12 +z/12 =1 ⇔ x +y +z -12 =0

Bài 11: Trong không gian với hệ trục tọa độ Oxyz, gọi (P) là mặt phẳng chứa trục Oy và tạo với mặt phẳng (Q): y + z + 1 = 0 góc 60⁰. Phương trình mặt phẳng (P) là:

   A.

   B.

   C.

   D.

Lời giải:

Đáp án : C

Giải thích :

Gọi n→ (a;b;c) là vecto pháp tuyến của mặt phẳng (P)

Mặt phẳng (Q) có vecto pháp tuyến n₁→ =(0;1;1), trục Oy có vecto chỉ phương

u→=(0;1;0)

Do mặt phẳng (P) chứa trục Oy nên n→. u→=0 ⇔ b=0

Mặt phẳng (P) tạo với mặt phẳng (Q) góc 60⁰

⇒ cos ⁡ 60⁰= =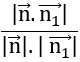

⇔ 1/2=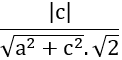 ⇔ a=±c

Chọn a = 1 ⇒ c=±1. Khi đó, phương trình mặt phẳng (P) đi qua điểm O(0; 0; 0) và có vecto pháp tuyến n→ là:

Bài 12: Trong không gian với hệ toạ độ Oxyz, cho hình cầu (S): (x - 1)² +(y - 2)² +(z - 3)² = 1. Phương trình mặt phẳng (α) chứa trục Oz và tiếp xúc với (S)

   A.

   B.

   C.

   D.

Lời giải:

Đáp án : D

Giải thích :

Gọi n→ (a;b;c) là vecto pháp tuyến của mặt phẳng (P)

Trục Oz có vecto chỉ phương u→=(0;0;1) và đi qua điểm O(0; 0; 0)

Do mặt phẳng (P) chứa trục Oz nên n→. u→=0 ⇔ c=0

Phương trình mặt phẳng (P) có vecto pháp tuyến n→ (a;b;0) và đi qua O là:

ax +by=0

Mặt cầu (S) có tâm I (1; 2; 3) và bán kính R = 1.

Do mặt phẳng (P) tiếp xúc với mặt cầu S nên d(I;(P))=R

=1 ⇔ a² +4ab +4b² =a² +b²

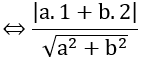
Với b = 0, chọn a= 1 ⇒ phương trình mặt phẳng (P) là x = 0

Với a=(-3/4)b, chọn b= -4 ⇒ a=3,

Phương trình mặt phẳng (P) là: 3x -4y =0

Bài 13: Trong không gian với hệ toạ độ Oxyz, cho hình cầu (S): (x - 1)² + (y - 2)² + (z - 3)² = 16. Phương trình mặt phẳng (α) chứa Oy cắt hình cầu (S) theo thiết diện là đường tròn có chu vi bằng 8π

   A. (α): 3x + z =0

   B. (α): 3x - z =0

   C. (α): 3x + z +2 =0

   D. (α): x - 3z =0

Lời giải:

Đáp án : B

Giải thích :

Gọi n→ (a;b;c) là vecto pháp tuyến của mặt phẳng (P)

Trục Oy có vecto chỉ phương u→=(0;1;0) và đi qua điểm O(0; 0; 0)

Do mặt phẳng (P) chứa trục Oz nên n→. u→=0 ⇔ b=0

Phương trình mặt phẳng (P) có vecto pháp tuyến n→(a;0;c) và đi qua O là:

ax +cz =0

Mặt cầu (S) có tâm I (1; 2; 3) và bán kính R = 4.

Mặt phẳng cắt mặt cầu theo thiết diện là đường tròn chu vi bằng

⇒ Bán kính của thiết diện là 4

⇒ Mặt phẳng (P) đi qua tâm I của mặt cầu (S)

Khi đó, ta có: a +3c=0 ⇔ a= -3c

Chọn c= -1 ⇒ a=3

Vậy phương trình mặt phẳng (P) là: 3x -z=0

Bài 14: Trong không gian với hệ trục tọa độ Oxyz, gọi (P) là mặt phẳng song song với mặt phẳng Oxz và cắt mặt cầu (x - 1)² + (y + 2)² + z² = 12 theo đường tròn có chu vi lớn nhất. Phương trình của (P) là:

   A. y +2 =0

   B. y -2 =0

   C. y +1 =0

   D. x -2y +1 =0

Lời giải:

Đáp án : A

Giải thích :

Mặt phẳng (P) song song với mặt phẳng Oxz nên mặt phẳng (P) có dạng:

y +D =0 (D≠0)

Mặt cầu có tâm I (1; -2; 0) và bán kính R=2√3

Mặt phẳng cắt mặt cầu theo đường tròn có chu vi lớn nhất ⇔ Mặt phẳng (P) đi qua tâm I

⇒ -2 +D =0 ⇔ D=2

Vậy phương trình mặt phẳng (P) là y +2 =0

Bài 15: Trong không gian Oxyz. Phương trình mặt phẳng (α) đi qua A(-1 ;2 ;4) và song song với mặt phẳng (P): 2x - 4y + 5z - 15 = 0

   A. (α): 2x - 4y + 5z + 10 = 0

   B. (α): 2x - 4y + 5z - 5 = 0

   C. (α): 2x - 4y + 5z - 10 = 0

   D. (α): 2x - 4y + 5z + 5 = 0

Lời giải:

Đáp án : C

Giải thích :

Phương trình mặt phẳng (α) song song với mặt phẳng (P) : 2x – 4y + 5z – 15 =0 có dạng :

⇒ 2x -4y +5z +D =0 (D≠ -15)

Do mặt phẳng (α) đi qua điểm A (-1 ; 2 ; 4) nên ta có :

2 .(-1) -4 .2 +5 .4 +D =0 ⇒ D= -10

Vậy phương trình mặt phẳng cần tìm là : 2x -4y +5z -10 =0

Bài 16: Trong không gian Oxyz cho ba điểm A(3;0;0), B(-1;1;1), C(-3;1;2). Phương trình của mặt phẳng (ABC) là :

   A. 2x + y + 2z - 2 = 0

   B. x + 2y + 2z - 3 = 0

   C. x + 2y + z - 3 = 0

   D. x - 2y + 2z - 3 = 0

Lời giải:

Đáp án : B

Giải thích :

AB→=(-4;1;1); AC→=(-6;1;2)

⇒ [AB→ , AC→ ]=(1;2;2)

Phương trình mặt phẳng (ABC) nhận n→=[AB→ , AC→ ]=(1;2;2) làm vecto pháp tuyến và đi qua A (3; 0; 0) là:

x +2y +2z -3 =0

Bài 17: Trong không gian với hệ trục tọa độ Oxyz, cho các điểm A(5;1;3), B(1;2;6), C(5;0;4). Viết phương trình mặt phẳng chứa AB và song song với CD.

   A. x + y + z - 9 = 0

   B. 2x - y + 3z + 6 = 0

   C. 2x - y + z + 4 = 0

   D. 2x + 5y + z - 18 = 0

Lời giải:

Đáp án : D

Giải thích :

AB→ =(-4;1;3); CD→=(-1;0;2)

⇒ [AB→ , CD→ ]=(2;5;1)

Phương trình mặt phẳng (P) chứa AB và song song với CD nhận n→=[AB→ , CD→ ]=(2;5;1) làm vecto pháp tuyến và đi qua A (5;1;3) là:

2(x -5) +5(y -1) +z -3 =0

⇔ 2x +5y +z -18 =0

Bài 18: Trong không gian Oxyz cho 2 điểm A(4;-1;3), B(-2;3;1). Phương trình mặt phẳng trung trực của đoạn thẳng AB là

   A. 3x - 2y + z + 3 = 0

   B. - 6x + 4y - 2z - 6 = 0

   C. 3x - 2y + z - 3 = 0

   D. 3x - 2y - z + 1 = 0

Lời giải:

Đáp án : C

Giải thích :

Mặt phẳng (P) đi qua trung điểm I (1; 1; 2) của AB và vuông góc với AB nên nhận

AB→=(-6;4; -2) làm vecto pháp tuyến.

Phương trình mặt phẳng (P) là: -6(x -1) +4(y -1) -2(z -2) =0

⇔ 3x -2y +z -3 =0

Bài 19: Trong không gian với hệ trục tọa độ Oxyz, gọi (P) là mặt phẳng chứa trục Ox và vuông góc với mặt phẳng (Q): x + y + z - 3 = 0. Phương trình mặt phẳng (P) là:

   A. y - z = 0

   B. y + z = 0

   C. y - z - 1 = 0

   D. y - 2z = 0

Lời giải:

Đáp án : A

Giải thích :

Trục Ox có vecto chỉ phương u→=(1;0;0) và đi qua điểm O (0; 0; 0)

Mặt phẳng (Q) có vecto pháp tuyến n_Q→=(1;1;1)

[u→ , n_Q→ ]=(0;-1;1)

Mặt phẳng (P) chứa trục Ox và vuông góc với mặt phẳng (Q) nên nhận vecto

n→= -[u→ , n_Q→ ]=(0;1; -1) làm vecto pháp tuyến

Phương trình mặt phẳng (P) nhận n→ làm vecto pháp tuyến và đi qua O(0; 0; 0) là:

y -z =0

Bài 20: Trong không gian với hệ trục tọa độ Oxyz. Phương trình của mặt phẳng chứa trục Ox và qua điểm I(2;-3;1) là:

   A. y + 3z = 0

   B. 3x + y = 0

   C. y - 3z = 0

   D. 3y + z = 0

Lời giải:

Đáp án : A

Giải thích :

Trục Ox có vecto chỉ phương u→=(1;0;0) và đi qua điểm O (0; 0; 0)

OI→=(2; -3;1)

⇒ [OI→ , u→]=(0;1;3)

Do mặt phẳng (P) chứa trục Ox và đi qua I(2; -3; 1) nên mặt phẳng (P) nhận

n→=[OI→ , u→]=(0;1;3) làm vecto pháp tuyến.

Phương trình mặt phẳng (P) là: y +3z =0

Bài 21: Trong không gian với hệ tọa độ Oxyz, cho tứ diện ABCD có các đỉnh A(1;2;1), B(-2;1;3), C(2;-1;3) và D(0;3;1). Phương trình mặt phẳng (α) đi qua A, B đồng thời cách đều C, D

   A. (P₁): 3x + 5y + 7z - 20 = 0; (P₂): x + + 3y + 3z - 10 = 0

   B. (P₁): 6x - 4y + 7z - 5 = 0; (P₂): 3x + y + 5z + 10 = 0

   C. (P₁): 6x - 4y + 7z - 5 = 0; (P₂): 2x + 3z - 5 = 0

   D. (P₁): 4x + 2y + 7z - 15 = 0; (P₂): x - 5y - z + 10 = 0

Lời giải:

Đáp án : A

Giải thích :

AB→=(-3; -1;2); CD→=(-2;4; -2)

Gọi n→ là vecto pháp tuyến của mặt phẳng (α)

Do mặt phẳng (α) cách đều C, D nên xảy ra 2 trường hợp

TH1: CD song song với mặt phẳng (α)

Khi đó: n→=[AB→ , CD→ ]=(-6; -10; -14)= -2(3;5;7)

Phương trình mặt phẳng (α) là:

3(x -1)+5(y -2) +7(z -1) =0

⇔ 3x +5y +7z -20 =0

TH2: Mặt phẳng (α) cắt CD tại trung điểm I của CD

I(1;1;2) ⇒ AI→=(0; -1;1)

Do I thuộc (α) nên n→=[AB→ ; AI→]=(1;3;3)

Phương trình mặt phẳng (α) là:

x -1+3(y -2)+3(z -1) =0

⇔ x +3y +3z -10 =0

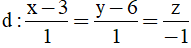
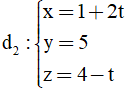
Bài 22: Trong không gian Oxyz cho điểm A(1;0;0) và hai đường thẳng; . Phương trình mặt phẳng qua A và song song với d₁ và d₂ là

   A. x + y + z - 1 = 0

   B. 2x + y + 2z - 1 = 0

   C. x + y + 2z - 1 = 0

   D. 3x + 2y + z - 3 = 0

Lời giải:

Đáp án : C

Giải thích :

Đường thẳng d₁ có vecto chỉ phương u₁→=(1 ;1 ; -1)

Đường thẳng d₂ có vecto chỉ phương u₂→=(2 ;0 ; -1)

Mặt phẳng (P) song song với d₁ và d₂ nên mặt phẳng (P) có vecto pháp tuyến

n→=[u₁→ ; u₂→ ]=(-1;-1; -2)= -(1;1;2)

Phương trình mặt phẳng (P) có vecto pháp tuyến n→=(1;1;2) và đi qua A (1 ; 0 ; 0) là:

x +y +2z -1 =0.

Bài 23: Trong không gian với hệ trục tọa độ Oxyz, cho điểm G(1;4;3). Viết phương trình mặt phẳng cắt các trục Ox, Oy, Oz lần lượt tại A, B, C sao cho G là trọng tâm tứ diện OABC ?

   A.

   B.

   C.

   D.

Lời giải:

Đáp án : D

Giải thích :

Goi A(a; 0; 0); B(0; b; 0); C(0; 0; c)

G(1; 4; 3) là trọng tâm của tứ diện OABC.

Phương trình mặt phẳng (ABC) là:

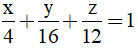
Bài 24: Trong không gian với hệ trục tọa độ Oxyz, cho hai mặt phẳng có phương trình (P): x + 2y + 2z - 1 = 0, (Q): x + 2y - z - 3 = 0 và mặt cầu (S): (x - 1)² +(y + 2)² +z² = 5 .Mặt phẳng (α) vuông với mặt phẳng (P), (Q) đồng thời tiếp xúc với mặt cầu (S).

   A. 2x - y + 1 = 0 Λ 2x - y - 9 = 0

   B. 2x - y - 1 = 0 Λ 2x - y + 9 = 0

   C. x - 2y + 1 = 0 Λ x - 2y - 9 = 0

   D. 2x + y - 1 = 0 Λ 2x + y + 9 = 0

Lời giải:

Đáp án : A

Giải thích :

Mặt phẳng (P) có vecto pháp tuyến n₁→=(1;2;2)

Mặt phẳng (Q) có vecto pháp tuyến n₂→=(1;2;-1)

Mặt cầu (S) có tâm I (1; -2; 0), bán kính R=√5.

Gọi n→ là vecto pháp tuyến của mặt phẳng (α).Do mặt phẳng (α) vuông góc với mặt phẳng (P), (Q) nên n→=[n₁→ ; n₂→ ]=(-6;3;0)= -3(2; -1;0)

Phương trình mặt phẳng (α) có dạng: 2x -y + D =0

Do mặt phẳng (α) tiếp xúc với mặt cầu (S) nên d(I;(α))=R

=√5

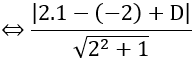
⇒ |4+D|=5 ⇔

Vậy phương trình mặt phẳng (α) là

2x -y +1=0

2x -y -9 =0

Bài 25: Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng (P): x + 2y - 2z + 1 = 0, 2 điểm A(1;0;0), B(-1;2;0), (S): (x - 1)² + (y - 2)² +z² = 25. Viết phương trình mặt phẳng (α) vuông với mặt phẳng (P), song song với đường thẳng AB, đồng thời cắt mặt cầu (S) theo đường tròn có bán kính bằng r=2√2

   A. 2x - 2y + 3z + 11 = 0 Λ 2x - 2y + 3z - 23 = 0

   B. 2x + 2y + 3z + 11 = 0 Λ 2x + 2y + 3z - 23 = 0

   C. 2x - 2y + 3z - 11 = 0 Λ 2x - 2y + 3z + 23 = 0

   D. 2x + 2y + 3z - 11 = 0 Λ 2x + 2y + 3z + 23 = 0

Lời giải:

Đáp án : B

Giải thích :

Mặt phẳng (P) có vecto pháp tuyến n₁→=(1;2; -2)

AB→=(-2;2;0)

Gọi n→ là vecto pháp tuyến của mặt phẳng (α)

Do mặt phẳng (α) vuông với mặt phẳng (P), song song với đường thẳng AB nên

n→=[n₁→ ; AB→ ]=(4;4;6)= 2(2; 2; 3)

Phương trình mặt phẳng (α) có dạng:

2x +2y +3z +D =0

Mặt cầu (S) có tâm I (1; 2; 0) bán kính R=5

Gọi khoảng cách từ tâm I đến mặt phẳng (P) là d

⇒ d=

Mặt phẳng (α) cắt mặt cầu (S) theo đường tròn có bán kính bằng r= 2√2 nên ta có:

d² +r² =R² ⇒ d=√(5² -(2√2)² )=√17

⇒ |D+6|/√17=√17 ⇔ |D+6|=17 ⇔

Vậy phương trình mặt phẳng (α) là:

2x +2y +3z +23 =0

2x +2y +3z -11 =0

Bài 26: Trong không gian Oxyz, Phương trình mặt phẳng (P) chứa trục Ox và vuông góc với mặt phẳng (Q): 3x + y - 2z - 5 = 0 là

   A. - x + 3y = 0

   B. 2x + 3y = 0

   C. 2y - z = 0

   D. 2y + z = 0

Lời giải:

Đáp án : D

Giải thích :

Trục Ox đi qua O (0; 0; 0) và có vecto chỉ phương u→=(1;0;0)

Mặt phẳng (Q) có vecto pháp tuyến n₁→=(3;1; -2)

Gọi n→ là vecto pháp tuyến của mặt phẳng (P)

Do mặt phẳng (P) chứa trục và vuông góc với mặt phẳng (Q) nên

n→=[u→ , n₁→ ]=(0;2;1)

Phương trình mặt phẳng (P) đi qua O và có vecto pháp tuyến n→ là:

2y +z =0

Bài 27: Trong không gian với hệ trục toạ độ Oxyz, cho hai mặt phẳng (P): x + y + z - 3 = 0, (Q): 2x + 3y + 4z - 1 = 0. Lập phương trình mặt phẳng (α) đi qua A(1;0;1) và chứa giao tuyến của hai mặt phẳng (P), (Q)

   A. (α): 7x + 8y + 9z - 16 = 0

   B. (α): 2x + 3y + z - 3 = 0

   C. (α): 7x + 8y + 9z - 17 = 0

   D. (α): 2x - 2y + z - 3 = 0

Lời giải:

Đáp án : A

Giải thích :

Mặt phẳng (P) có vecto pháp tuyến n₁→=(1;1;1)

Mặt phẳng (Q) có vecto pháp tuyến n₂→=(2;3;4)

Gọi d là giao tuyến của mặt phẳng (P) và (Q). Khi đó vecto chỉ phương u₁→ của đường thẳng d là:

u₁→=[n₁→ , n₂→ ]=(1; -2;1)

Gọi M(a;b;0) là điểm thuộc giao tuyến của (P) và (Q)

⇒ ⇔ ⇒ M(8; -5;0)

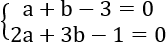
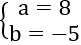
⇒ AM→=(7; -5; -1)

Gọi n→ là vecto pháp tuyến của mặt phẳng (α)

Phương trình mặt phẳng (α) đi qua A(1;0;1) và chứa giao tuyến của hai mặt phẳng nên n→=[u₁→ ; AM→ ]=(7;8;9)

Phương trình mặt phẳng (α) là: 7(x -1) +8y +9(z -1) =0

⇔ 7x +8y +9z -16 =0

Bài 28: Phương trình mặt phẳng (α) đi qua hai điểm A(3;1;-1), B(2;-1;4) và vuông góc với mặt phẳng có phương trình (β): 2x - y + 3z = 0 là :

   A. 2x - y +3z -2 = 0

   B. x -13y -5z + 5 = 0

   C. -x +13y + 5z = 0

   D. x -13y - 5z +6 = 0

Lời giải:

Đáp án : B

Giải thích :

AB→=(-1; -2;5)

Mặt phẳng (β) có vecto pháp tuyến n₁→=(2;-1;3)

Mặt phẳng (α) đi qua A, B và vuông góc với mặt phẳng (β) nên mặt phẳng (α) có vecto pháp tuyến là n→=[AB→ , n₁→ ]=(-1 ;13 ;5)

Phương trình mặt phẳng (α) đi qua A (3 ; 1 ; -1) và có vecto pháp tuyến n→ là :

-(x -3) +13(y -1) +5(z +1) =0

⇔ -x +13y +5z -5 =0

⇔ x -13y -5z +5 =0

Bài 29: Phương trình mặt phẳng (P) đi qua M(3;-1;-5), đồng thời vuông góc với cả hai mặt phẳng (Q): 3x -2y+2z = 0 và (R): 5x-4y+3z=0 là :

   A. 3x - y - 5z - 15 = 0

   B. 3x + y - 2z + 15 = 0

   C. 2x + 3y - 2z + 15 = 0

   D. 2x + y - 2z - 15 = 0

Lời giải:

Đáp án : D

Giải thích :

Mặt phẳng (Q) có vecto pháp tuyến n_Q→=(3 ; -2 ;2)

Mặt phẳng (P) có vecto pháp tuyến n_P→=(5 ; -4 ;3)

Mặt phẳng (P) vuông góc với (P) và (Q) nên vecto pháp tuyến của mặt phẳng (P) là

n→=[n_Q→ , n_P→ ]=(2; 1; -2)

Phương trình mặt phẳng (P) đi qua M(3 ; -1 ; -5) và có vecto pháp tuyến n→ là :

2(x -3) +(y +1) -2(z +5) =0

⇔ 2x +y -2z -15 =0

Bài 30: Phương trình (P) là mặt phẳng trung trực của đoạn MN với M=(1;-2;4), N=(3;6;2) là :

   A. x + 4y - z + 11=0

   B. x - 2y + z -5= 0

   C. x + 4y - z - 7 = 0

   D. x - 2y + z = 0

Lời giải:

Đáp án : C

Giải thích :

Gọi I là trung điểm của đoạn thẳng MN ⇒ I(2;2;3)

⇒ MI→=(1;4; -1)

Do (P) là mặt phẳng trung trực của MN nên mặt phẳng (P) đi qua I và nhận MI→ làm vecto pháp tuyến. Phương trình mặt phẳng (P) là:

x -2 +4(y -2) -(z -3) =0

⇔ x +4y -z -7 =0

Bài 31: Trong không gian Oxyz phương trình mặt phẳng (P) đi qua 2 điểm A(2;0;-1), B(1;-2;3) và vuông góc với mặt phẳng (Q): x - y + z + 1 = 0 là

   A. (P): 2x + 5y + 3z - 1 = 0

   B. (P): - 2x + 5y - 3z + 1 = 0

   C. (P): 2x + 5y + 3z - 7 = 0

   D. (P): - 2x + 5y - 3z + 7 = 0

Lời giải:

Đáp án : A

Giải thích :

AB→=(-1; -2;4)

Mặt phẳng (Q) có vecto pháp tuyến n_Q→=(1; -1;1)

Do Mặt phẳng (P) đi qua A, B và vuông góc với mặt phẳng (Q) nên vecto pháp tuyến của mặt phẳng (P) là: n→=[AB→ , n_Q→ ]=(2;5;3)

Phương trình mặt phẳng (P) đi qua A(2; 0; -1) và có vecto pháp tuyến n→ là:

2(x -2) +5y +3(z +1) =0

⇔ 2x +5y +3z -1 =0

Bài 32: Trong không gian Oxyz phương trình mặt phẳng (P) đi qua điểm A(1;-2;3) vuông góc với mặt phẳng (Q): x + 2y - z + 5 = 0 và song song với đường thẳng 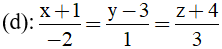là

   A. (P): 7x - y + 5z - 20 = 0

   B. (P): 7x - y + 5z - 24 = 0

   C. (P): x + 3y - 5z - 10 = 0

   D. (P): 3x + y + 5z - 20 = 0

Lời giải:

Đáp án : B

Giải thích :

Mặt phẳng (Q) có vecto pháp tuyến n_Q→=(1; 2;-1)

Đường thẳng d có vecto chỉ phương u→=(-2;1;3)

Do mặt phẳng (P) vuông góc với mặt phẳng (Q) và song song với đường thẳng (d) nên vecto pháp tuyến của mặt phẳng (P) là n→=[n_Q→ , u→ ]=(7;-1;5)

Phương trình mặt phẳng (P) có vecto pháp tuyến n→ và đi qua A(1; -2; 3) là:

7(x -1) -(y +2) +5(z -3) =0

⇔ 7x -y +5z -24 =0

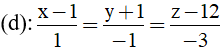
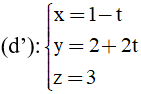
Bài 33: Trong không gian Oxyz phương trình mặt phẳng (P) chứa hai đường thẳng cắt nhau và là

   A. (P): 3x - 6y + 3z = 0

   B. (P): 6x + 3y + z + 15 = 0

   C. (P): 6x + 3y + z - 15 = 0

   D. (P): - 6x - 3y + 3z + 3 = 0

Lời giải:

Đáp án : C

Giải thích :

Đường thẳng d có vecto chỉ phương u₁→=(1; -1; -3) và đi qua điểm A (1; -1; 12)

Đường thẳng d’ có vecto chỉ phương u₂→=(-1;2;0)

Mặt phẳng (P) chứa d và d’ nên mặt phẳng (P) có vecto pháp tuyến là

n→=[u₁→ , u₂→ ]=(6;3;1)

Phương trình mặt phẳng (P) đi qua A(1; -1; 12) và có vecto pháp tuyến n→=(6;3;1)

6(x -1) +3(y +1) +z -12 =0

⇔ 6x +3y +z -15 =0

Bài 34: Trong không gian Oxyz cho mặt phẳng (Q): x + 2y +z -3 = 0 và đường thẳng 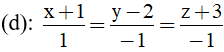. Viết phương trình mp (P) chứa (d) và hợp với mp (Q) một góc α thỏa mãn cos α= √3/6.

   A. (P): - 5x + 3y - 8z - 35 = 0

   B. (P): 5x - 3y + 8z - 15 = 0

   C. (P): 3x + 5y + 8z + 5 = 0

   D. (P): 8x - 5y + 3z - 1 = 0

Lời giải:

Đáp án : B

Giải thích :

Gọi vecto pháp tuyến của mặt phẳng (P) là n→(A;B;C)

Đường thẳng (d) đi qua điểm M(-1; 2; -3) có vecto chỉ phương u→=(1; -1; -1)

Do mặt phẳng (P) chứa d nên n→ .u→=0 ⇔ A -B -C =0 ⇔ A =B +C.

Mặt phẳng (Q) có vecto pháp tuyến n_Q→=(1;2;1)

Mặt phẳng (P) hợp với mặt phẳng (Q) góc α thỏa cos α = √3/6 nên ta có:

Với 8B = -3C, chọn C=8; B= -3 ⇒ A=5 ⇒ n→=(5; -3;8)

Với B= -C, chọn C=-1; B=1 ⇒ A=0 ⇒ n→=(0; 1;-1)

Khi đó, phương trình mặt phẳng (P) đi qua M(-1; 2; -3) và có vecto pháp tuyến n→ là:

5x -3y +8z -15 =0

y -z +1 =0

Bài 35: Trong không gian Oxyz viết phương trình mặt phẳng (P) chứa hai đường thẳng song song với nhau 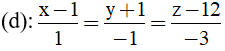và

   A. (P): 6x + 3y + z - 15 = 0

   B. (P): - 27x + 9y + 3z = 0

   C. (P): - 27x + 9y - 3z = 0

   D. (P): 6x + 3y + z + 15 = 0

Lời giải:

Đáp án : A

Giải thích :

Đường thẳng d đi qua A(1; -1; 12) và có vecto chỉ phương u→=(1; -1;-3)

Đường thẳng d’ đi qua B( 1; 2; 3)

AB→=(0; 3; -9)

Do mặt phẳng (P) chứa d và d’ song song với nhau nên vecto pháp tuyến của mặt phẳng (P) là n→=[AB→ , u→]=(6;3;1)

Khi đó phương trình mặt phẳng (P) là:

6(x -1) +3(y -2) +(z -3) =0

⇔ 6x +3t +z -15 =0

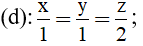
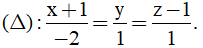
Bài 36: Trong không gian oxyz cho hai đường thẳng Phương trình mp (P) chứa (d) và song song với (Δ)

   A. (P): x + y - 3z = 0

   B. (P): - x + 3y - z = 0

   C. (P): x - 3y + 5z = 0

   D. (P): - x - 5y + 3z = 0

Lời giải:

Đáp án : D

Giải thích :

Đường thẳng d đi qua điểm O(0; 0; 0) và có vecto chỉ phương u₁→=(1;1;2)

Đường thẳng (Δ) có vecto chỉ phương u₂→=(-2;1;1)

Do mặt phẳng (P) chứa (d) và song song với (Δ) nên vecto pháp tuyến của mặt phẳng (P) là n→=[u₁→ , u₂→]=(-1; -5;3)

Phương trình mặt phẳng (P) là:

-x -5y +3z =0

Bài 37: Trong không gian với hệ toạ độ Oxyz, cho các điểm A(1;1;0), B(3;1;2). Phương trình mặt phẳng trung trực của đoạn AB là

   A. x + z - 4 = 0

   B. x + z - 2 = 0

   C. x + y - z - 2 = 0

   D. x + 2y - 2 = 0

Lời giải:

Đáp án : B

Giải thích :

I là trung điểm của AB ⇒ I(2;1;1)

AI→=(1; 0;1)

Khi đó mặt phẳng trung trực của AB nhận AI→=(1;0;1) và đi qua điểm I

Phương trình mặt phẳng cần tìm là: x +z -2 =0

Bài 38: Phương trình tổng quát (α) qua A(2;-1;4), B(3;2;-1) và vuông góc với (β): x + y + 2z - 3 = 0 là:

   A. 11x + 7y - 2z - 21 = 0

   B. 11x + 7y + 2z + 21 = 0

   C. 11x - 7y - 2z - 21 = 0

   D. 11x - 7y + 2z + 21 = 0

Lời giải:

Đáp án : C

Giải thích :

Ta có: AB→=(1;3; -5)

Mặt phẳng (β) có vecto pháp tuyến n₁→=(1;1;2)

Do mặt phẳng (α) đi qua A, B và vuông góc với (β) nên vecto pháp tuyến của mặt phẳng (α) là: n→=[ AB→ , n₁→ ]=(11; -7; -2)

Phương trình mặt phẳng (α) là:

11(x -2) -7(y +1) -2(z -4) =0

⇔ 11x -7y -2z -21=0

Bài 39: Trong không gian với hệ toạ độ Oxyz, cho điểm M(8;-2;4). Gọi A, B, C lần lượt là hình chiếu của M trên các trục Ox, Oy, Oz. Phương trình mặt phẳng đi qua ba điểm A, B và C là

   A. x + 4y + 2z - 8 = 0

   B. x - 4y + 2z - 8 = 0

   C. x - 4y - 2z - 8 = 0

   D. x + 4y - 2z - 8 = 0

Lời giải:

Đáp án : B

Giải thích :

A, B, C lần lượt là hình chiếu của M(8; -2; 4) trên các trục Ox, Oy, Oz

⇒ A(8;0;0), B(-2;0;0), C(4;0;0)

Phương trình mặt phẳng đi qua 3 điểm A, B, C là:

x/8 -y/2 +z/4 =1 ⇔ x -4y +2z -8 =0

Bài 40: Mặt phẳng (α) đi qua M(0;0;-1) và song song với giá của hai vectơ a→(1;-2;3) và b→(3;0;5). Phương trình của mặt phẳng (α) là

   A. - 5x + 2y + 3z + 3 = 0

   B. 5x - 2y - 3z - 21 = 0

   C. 10x - 4y - 6z + 21 = 0

   D. 5x - 2y - 3z + 21 = 0

Lời giải:

Đáp án : A

Giải thích :

Do mặt phẳng (α) song song với giá của hai vecto a→(1;-2;3) và b→(3;0;5) nên vecto pháp tuyến của mặt phẳng (α) là: n→=[ a→ , b→ ] =(-10;4;6)

Mặt phẳng (α) đi qua M (0; 0; -1) và có vecto pháp tuyến n→=(-10;4;6) là:

-10x +4y +6(z +1) =0

⇔ -5x +2y +3z +3 =0

Bài 41: Trong không gian với hệ toạ độ Oxyz, cho mặt phẳng (P) đi qua hai điểm A(4;-1;1), B(3;1;-1) và song song với trục Ox. Phương trình nào sau đây là phương trình của mặt phẳng (P)

   A. x + y + z = 0

   B. x + y = 0

   C. y + z = 0

   D. x + z = 0

Lời giải:

Đáp án : C

Giải thích :

Ta có: AB→=(-1;2; -2)

Trục Ox có vecto chỉ phương u→=(1;0;0)

Do mặt phẳng (P) đi qua A, B và song song với trục Ox nên vecto pháp tuyến của mặt phẳng (P) là n→=[ AB→ , u→ ] =(0; -2; -2)= -2(0;1;1)

Phương trình mặt phẳng (P) đi qua A và có vecto pháp tuyến n→ là:

y +1 +z -1 =0 ⇔ y +z =0

Bài 42: Trong không gian với hệ toạ độ Oxyz, cho mặt phẳng (Q) song song với mặt phẳng (P): x + 2y + z - 4 = 0 và cách D(1;0;3) một khoảng bằng √6 có phương trình là

   A. x + 2y + z + 2 = 0

   B. x + 2y - z - 10 = 0

   C. x + 2y + z - 10 = 0

   D. x + 2y + z + 2 = 0 và x + 2y + z - 10 = 0

Lời giải:

Đáp án : D

Giải thích :

Do mặt phẳng (Q) song song với mặt phẳng nên mặt phẳng (Q) có dạng: x +2y +z +D =0 (D≠ -4)

Mặt phẳng (P) cách D một khoảng bằng nên ta có phương trình

=√6

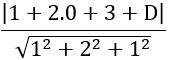
⇔ |4+D|=6 ⇔

Vậy phương trình mặt phẳng (P) là:

x +2y +z -2 =0

x +2y +z +10 =0

Bài 43: Trong không gian Oxyz, phương trình mặt phẳng (P) chứa trục Ox và cắt mặt cầu (S): x² + y² + z² - 2x + 4y + 2z - 3 = 0 theo một đường tròn (C) có bán kính bằng 3 là

   A. x - 2y - z = 0

   B. - y - 2z = 0

   C. y - 2z = 0

   D. Đáp số khác

Lời giải:

Đáp án : A

Giải thích :

Trục Ox có vecto chỉ phương u→=(1;0;0)

Mặt cầu (S) có tâm I (1; -2; -1) và bán kính R = 3

Do mặt phẳng (P) cắt mặt cầu (S) theo đường tròn (C) có bán kính bằng 3 nên mặt phẳng (P) đi qua tâm I của mặt cầu.

⇒ Mặt phẳng (P) đi qua O (0; 0; 0) và nhận OI→=(1; -2; -1) làm vecto pháp tuyến

Phương trình mặt phẳng (P) là: x -2y -z =0

Bài 44: Trong không gian với hệ toạ độ Oxyz mặt phẳng (P) đi qua B(0;-2;3), song song với đường thẳng 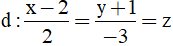và vuông góc với mặt phẳng (Q): x + y - z = 0 có phương trình là

   A. 2x - 3y + 5z - 9 = 0

   B. - 2x - 3y + 5z - 9 = 0

   C. 2x + 3y - 5z - 9 = 0

   D. 2x + 3y + 5z - 9 = 0

Lời giải:

Đáp án : D

Giải thích :

Đường thẳng (d) có vecto chỉ phương u→=(2; -3;1)

Mặt phẳng (Q) có vecto pháp tuyến n_Q→=(1;1; -1)

Do mặt phẳng (P) song song với đường thẳng d và vuông góc với mặt phẳng (Q) nên vecto pháp tuyến của mặt phẳng (P) là:

n→=[u→ , n_Q→ ]=(2;3;5)

Phương trình mặt phẳng (P) đi qua B(0; -2; 3) và có vecto pháp tuyến n→ là:

2x +3(y +2) +5(z -3) =0

⇔ 2x +3y +5z -9 =0

Bài 45: Trong không gian với hệ toạ độ Oxyz, cho điểm A(1;2;-2) và đường thẳng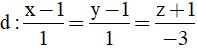 . Phương trình mp (P) chứa đường thẳng d và đi qua điểm A là

   A. x + y + 2z - 2 = 0

   B. 2x + y + 2z - 3 = 0

   C. x + 2y + 2z - 2 = 0

   D. 2x + y + z - 2 = 0

Lời giải:

Đáp án : A

Giải thích :

Đường thẳng d có vecto chỉ phương u→=(1;1; -3) và đi qua điểm M(1; 1; -1)

Ta có AM→=(0; -1; 1)

⇒ [ AM→ , u→ ]=(-2; -1; -1)= -(2;1;1)

Mặt phẳng (P) chứa d và đi qua A nên nhận n→= -([ AM→ , u→])=(2;1;1) làm vecto pháp tuyến

Phương trình mặt phẳng (P) là: 2(x -1) +y -2 +z -2 =0

⇔ 2x +y +z -2 =0

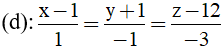
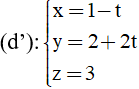
Bài 46: Trong không gian Oxyz phương trình mặt phẳng (P) chứa hai đường thẳng cắt nhau vàlà

   A. (P): 6x + 3y + z + 15 = 0

   B. (P): 6x + 3y + z - 15 = 0

   C. (P): 3x - 6y + 3z = 0

   D. (P): - 6x - 3y + 3z + 3 = 0

Lời giải:

Đáp án : B

Giải thích :

Đường thẳng (d) đi qua A (1; -1; 12) và có vecto chỉ phương là u₁→=(1; -1; -3)

Đường thẳng (d’) có vecto chỉ phương là u₂→=(-1; 2; 0)

Do mặt phẳng (P) chứa hai đường thẳng nên ta có vecto chỉ phương của mặt phẳng (P) là:

n→=[u₁→ , u₂→ ]=(6;3;1)

Phương trình mặt phẳng (P) cần tìm là: 6(x -1) +3(z +1) +z -12 =0

⇔ 6x +3y +z -15 =0

Bài 47: Trong không gian Oxyz cho đường thẳng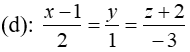 và điểm A(3;1;1). Viết pt mp (P) chứa (d) và d (A, (P))= 2√3.

   A. (P₁): x + y + z + 1 = 0 và (P₂): 7x + 3y + z - 3 = 0

   B. (P₁): x + y + z - 1 = 0 và (P₂): 7x + 5y - z + 3 = 0

   C. (P₁): x + y + z + 1 = 0 và (P₂): 7x + 5y + z + 3 = 0

   D. (P₁): x - y - z + 1 = 0 và (P₂): x + y - z + 3 = 0

Lời giải:

Đáp án : C

Giải thích :

Đường thẳng (d) đi qua điểm M(1; 0; -2) và có vecto chỉ phương u→=(2;1; -3)

Gọi phương trình mặt phẳng (P) là Ax + By +Cz + D =0.

Do mặt phẳng (P) chứa (d) nên ta có:

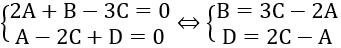
Ta có: d(A;(P))=2√3

⇒ =2√3

⇔ =2√3

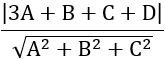
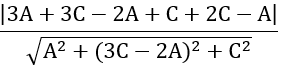
Vậy phương trình mặt phẳng (P) là: x +y +z +1 =0

7x +5y +z +3 =0

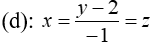
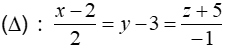
Bài 48: Trong không gian Oxyz cho hai đường thẳng (d) và (Δ) lần lượt có phương trình: và . Viết phương trình mặt phẳng (P) chứa (d) và hợp với (Δ) một góc 30⁰.

   A. (P₁): x + 2y + z - 4 = 0 và (P₂): x - z = 0

   B. (P₁): x + y - 2 = 0 và (P₂): x - y - 2z + 2 = 0

   C. (P₁): x - 2y + z - 4 = 0 và (P₂): x + z = 0

   D. (P₁): x + y - 2 = 0 và (P₂): x + z = 0

Lời giải:

Đáp án : D

Giải thích :

Đường thẳng (d) đi qua điểm M(0; 2; 0) và có vecto chỉ phương u₁→=(1;-1; 1)

Đường thẳng có vecto chỉ phương u₂→=(2;1; -1)

Gọi phương trình mặt phẳng (P) là Ax + By +Cz + D =0.

Do mặt phẳng (P) chứa (d) nên ta có:

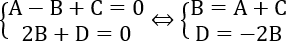
Mặt phẳng (P) hợp với góc 30⁰ nên ta có:

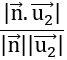
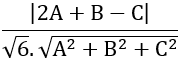
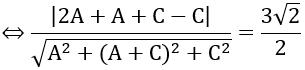
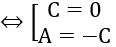
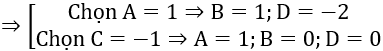
cos ⁡ 30⁰ = ⇔ =√3/2

Vậy phương trình mặt phẳng (P) là: x +y -2 =0

x -z =0

Bài 49: Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) có phương trình (x - 1)² + (y - 2)² + (z + 1)² = 1, phương trình mặt phẳng (Q) chứa trục hoành và tiếp xúc với mặt cầu (S) là

   A. (Q): 4y + 3z = 0

   B. (Q): 4y + 3z + 1 = 0

   C. (Q): 4y - 3z + 1 = 0

   D. (Q): 4y - 3z = 0

Lời giải:

Đáp án : A

Giải thích :

Gọi phương trình mặt phẳng (Q) là Ax +By +Cz +D =0

Mặt cầu (S) có tâm I(1; 2; -1) và bán kính R =1

Do mặt phẳng (Q) chứa Ox nên mặt phẳng (P) đi qua O và vecto pháp tuyến của (Q) vuông góc với vecto chỉ phương của Ox

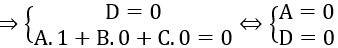
Phương trình mặt phẳng (Q) có dạng: By + Cz = 0

Do mặt phẳng (Q) tiếp xúc với mặt cầu (S) nên ta có: d(I, (Q))=R

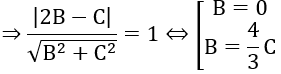
Với B=0,chọn C=1 ⇒ phương trình mặt phẳng z =0

Với B=4/3 C,chọn C=3, B=4 ⇒ phương trình mặt phẳng: 4y +3z =0

Bài 50: Trong không gian với hệ trục Oxyz, cho mặt phẳng (P) qua M(0;1;-3) song song với mặt phẳng (Q) có phương trình 2x -y +3z -5 =0 có phương trình là:

   A. - 2x + y - 3z - 10 = 0

   B. 2x - y + 3z - 10 = 0

   C. x - 2y + 3z + 1 = 0

   D. 2x + y - 3z - 10 = 0

Lời giải:

Đáp án : A

Giải thích :

Do mặt phẳng (P) song song với mặt phẳng (Q) nên phương trình mặt phẳng (P) có dạng: 2x -y +3z +D =0(D ≠ -5)

Do mặt phẳng (P) đi qua M (0; 1; -3) nên ta có:

2 .0 -1 +3 .(-3) +D =0 ⇒ D=10

Phương trình mặt phẳng (P) là 2x -y +3z +10 =0

Hay: - 2x + y - 3z - 10 = 0