Các dạng bài toán về lãi suất ngân hàng và cách giải

---

Các dạng bài toán về lãi suất ngân hàng và cách giải

Với Các dạng bài toán về lãi suất ngân hàng và cách giải Toán lớp 12 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập tiếp tuyến của đồ thị hàm số từ đó đạt điểm cao trong bài thi môn Toán lớp 12.

I. LÝ THUYẾT VÀ PHƯƠNG PHÁP GIẢI

1. Lãi đơn

Số tiền lãi chỉ tính trên số tiền gốc mà không tính trên số tiền lãi do số tiền gốc sinh ra.

Công thức tính lãi đơn: V_n = V₀(1 + r.n)

Trong đó:

V_n : tiền cả vốn lẫn lãi sau n kỳ hạn;

V₀ : Số tiền gửi ban đầu;

n : Số kỳ hạn tính lãi;

r : Lãi suất định kỳ, tính theo %.

2. Lãi kép

Là số tiền lãi không chỉ tính trên số tiền gốc mà còn tính trên số tiền lãi do tiền gốc đó sinh ra thay đổi theo từng định kỳ.

a. Lãi kép, gửi một lần: T_n = T₀(1 + r)ⁿ

Trong đó:

T_n : Số tiền cả vốn lẫn lãi sau n kỳ hạn;

T₀ : Số tiền gửi ban đầu;

n : Số kỳ hạn tính lãi;

r : Lãi suất định kỳ, tính theo %.

b. Lãi kép liên tục: T_n = T₀.e^n.r

Trong đó:

T_n : Số tiền cả vốn lẫn lãi sau n kỳ hạn;

T₀ : Số tiền gửi ban đầu;

n : Số kỳ hạn tính lãi;

r : Lãi suất định kỳ, tính theo %.

c. Lãi kép, gửi định kỳ.

• Trường hợp gửi tiền định kì cuối tháng.

Bài toán 1: Cứ cuối mỗi tháng gửi vào ngân hàng m triệu, lãi suất kép r% (tháng hoặc năm). Hỏi sau n (tháng hoặc năm) số tiền thu được là bao nhiêu?

Người ta chứng minh được số tiền thu được là:

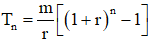
Chứng minh

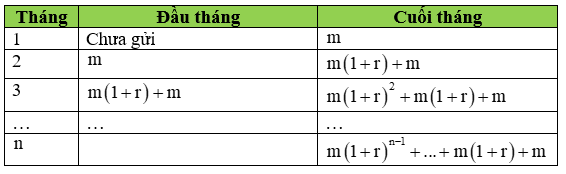
Vậy sau tháng n ta được số tiền

T_n = m(1 + r)^n-1 +....+ m(1 + r) + m = m[(1 + r)^n-1 +.....+(1 + r) + 1 ],

Ta thấy trong ngoặc là tổng u₁ = 1, u_n = (1 + r)^n-1, q = 1 + r số hạng của cấp số nhân có

Ta biết rằng: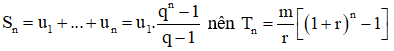

Bài toán 2: Cứ cuối mỗi tháng gửi vào ngân hàng m triệu, lãi suất kép r% (tháng hoặc năm). Sau n (tháng hoặc năm) số tiền thu được là A triệu. Hỏi số tiền gửi mỗi tháng m là bao nhiêu?

Người ta chứng minh được số tiền cần gửi mỗi tháng là: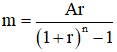

Chứng minh:

Áp dụng bài toán 1 ta có số tiền thu được là 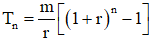, mà đề cho số tiền đó chính là A nên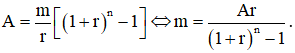

Bài toán 3: Cứ cuối mỗi tháng gửi vào ngân hàng m triệu, lãi suất kép r% (tháng hoặc năm). Sau n (tháng hoặc năm) số tiền thu được là A triệu. Hỏi số tháng hoặc năm n là bao nhiêu?

Người ta chứng minh được số tháng thu được đề bài cho là: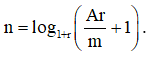

Chứng minh:

Áp dụng bài toán 1 ta có số tiền thu được là 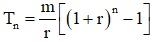, mà đề cho số tiền đó chính là A nên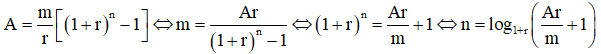

Như vậy trong trường hợp một này ta cần nắm vứng công thức Bài toán 1 từ đó có thể dễ dàng biến đổi ra các công thức ở bài toán 2, Bài toán 3.

• Trường hợp gửi tiền định kì đầu tháng.

Bài toán 4: Cứ đầu mỗi tháng gửi vào ngân hàng m triệu, lãi suất kép r% (tháng hoặc năm). Hỏi sau n (tháng hoặc năm) số tiền thu được là bao nhiêu?

Người ta chứng minh được số tiền thu được là: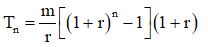

Chứng minh.

Ta xây dựng bảng sau:

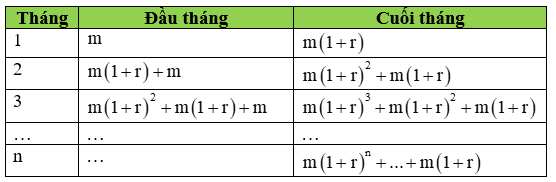
Vậy sau tháng n ta được số tiền:

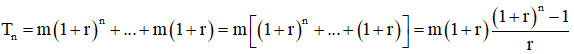
Bài toán 5: Cứ đầu mỗi tháng gửi vào ngân hàng m triệu, lãi suất kép r% (tháng hoặc năm). Sau n (tháng hoặc năm) số tiền thu được là A triệu. Hỏi số tiền gửi mỗi tháng m là bao nhiêu?

Người ta chứng minh được số tiền cần gửi mỗi tháng là: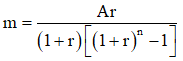

Chứng minh

Áp dụng bài toán 4. Ta có số tiền thu được là: 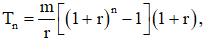mà đề cho số tiền đó là A nên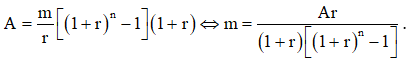

Bài toán 6: Cứ đầu mỗi tháng gửi vào ngân hàng m triệu, lãi suất kép r% (tháng hoặc năm). Sau n (tháng hoặc năm) số tiền thu được là A triệu. Hỏi số tháng hoặc năm n là bao nhiêu?

Người ta chứng minh được số tháng thu được đề bài cho là: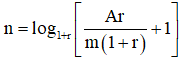

Chứng minh

Áp dụng bài toán 4. Ta có: số tiền thu được là: 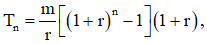mà đề cho số tiền đó là A nên .

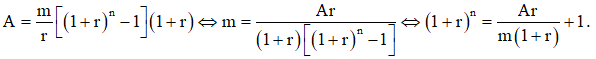
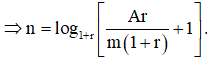
Như vậy trong trường hợp này ta cần nắm vững công thức bài toán 4 từ đó có thể dễ dàng biến đổi ra các công thức ở bài toán 5, bài toán 6.

• Trường hợp vay nợ và trả tiền định kì đầu tháng.

Bài toán 7: Vay ngân hàng A triệu đồng. Cứ đầu mỗi tháng (năm) trả ngân hàng m triệu, lãi suất kép r% (tháng hoặc năm). Hỏi sau n (tháng hoặc năm) số tiền còn nợ là bao nhiêu?

Người ta chứng minh được số tiền còn nợ là: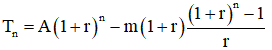

Chứng minh.

Ta xây dựng bảng sau:

Vậy sau tháng n ta còn nợ số tiền:

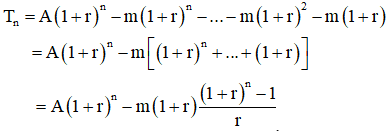
Trường hợp vay nợ và trả định kì cuối tháng.

Bài toán 8: Vay ngân hàng A triệu đồng. Cứ đầu mỗi tháng (năm) trả ngân hàng m triệu, lãi suất kép r% (tháng hoặc năm). Hỏi sau n (tháng hoặc năn) số tiền còn nợ là bao nhiêu?

Người ta chứng minh được số tiền còn nợ là: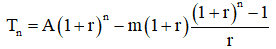

Chứng minh

Ta xây dựng bảng sau:

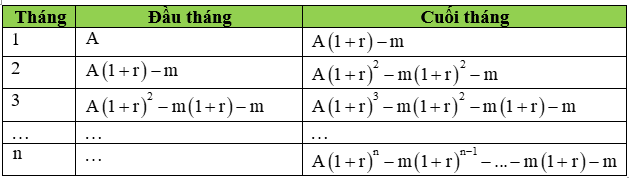
Vậy sau tháng n ta còn nợ số tiền:

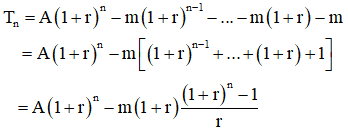
Sau đây cùng tìm hiểu cách áp dụng các lý thuyết vào các bài toán tính tiền lãi, tiền nợ phải trả như thế nào?

II. VÍ DỤ MINH HỌA

Câu 1: Đầu năm 2016, anh Hùng có xe công nông trị giá 100 triệu đồng. Biết mỗi tháng thì xe công nông hao mòn mất 0,4% giá trị, đồng thời làm ra được 6 triệu đồng ( số tiền làm ra mỗi tháng là không đổi). Hỏi sau một năm, tổng số tiền ( bao gồm giá tiền xe công nông và tổng số tiền anh Hùng làm ra ) anh Hùng có là bao nhiêu?

A. 172 triệu. B. 72 triệu.

C. 167,3042 triệu. D. 104,907 triệu.

Hướng dẫn giải

Chọn C.

Sau một năm số tiền anh Hùng làm ra là 6.12 = 72 triệu đồng

Sau một năm giá trị xe công nông còn 100(1 - 0,4%)¹² ≈ 95,3042 triệu đồng

Vậy sau một năm số tiền anh Hùng có là 167,3042 triệu đồng

Câu 2: Bác B gửi tiết kiệm số tiền ban đầu là 50 triệu đồng theo kỳ hạn 3 tháng với lãi suất 0,72% tháng. Sau một năm bác B rút cả vốn lẫn lãi và gửi theo kỳ hạn 6 tháng với lãi suất 0,78% tháng. Sau khi gởi đúng một kỳ hạn 6 tháng do gia đình có việc bác gửi thêm 3 tháng nữa thì phải rút tiền trước hạn cả gốc lẫn lãi được số tiền là 57 694 945,55 đồng (chưa làm tròn ). Biết rằng khi rút tiền trước hạn lãi suất được tính theo lãi suất không kỳ hạn, tức tính theo hàng tháng. Trong số 3 tháng bác gởi thêm lãi suất là

A. 0,55% . B. 0,3% C. 0,4% D. 0,5%

Hướng dẫn giải

Chọn C.

Số tiền bác B rút ra sau năm đầu: T₁ = 50000000.(1 + 0,00723)⁴

Số tiền bác B rút ra sau sáu tháng tiếp theo: T₂ = T₁(1 + 0,00786)

Số tiền bác B rút ra sau ba tháng tiếp theo:

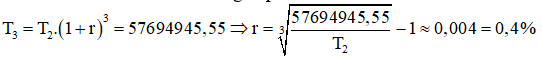
Câu 3: Bạn Nam là sinh viên của một trường Đại học, muốn vay tiền ngân hàng với lãi suất ưu đãi trang trải kinh phí học tập hàng năm. Đầu mỗi năm học, bạn ấy vay ngân hàng số tiến 10 triệu đồng với lãi suất là 4%. Tính số tiền mà Nam nợ ngân hàng sau 4 năm, biết rằng trong 4 năm đó, ngân hàng không thay đổi lãi suất ( kết quả làm tròn đến nghìn đồng).

A. 46794000 đồng. B. 44163000 đồng.

C. 42465000 đồng. D. 41600000 đồng.

Hướng dẫn giải

Chọn B.

Tổng số tiền bạn Nam vay ( gốc và lãi) sau 4 năm là:

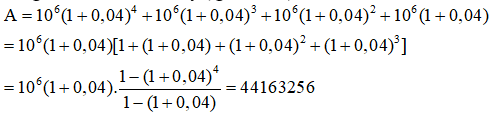
Nên A = 44163000 đồng

Câu 4: Một kỹ sư được nhận lương khởi điểm là 8 000 000 đồng/tháng. Cứ sau hai năm lương mỗi tháng của kỹ sư đó được tăng thêm 10% so với mức lương hiện tại. Tính tổng số tiền T (đồng) kỹ sư đó nhận được sau 6 năm làm việc.

A. 633 600 000. B. 635 520 000.

C. 696 960 000. D. 766 656 000.

Hướng dẫn giải

Chọn B.

Lương 2 năm đầu tiên của công nhân đó nhận được là T₁ = 8.10⁶.24 = 192.10⁶ (đồng)

Theo công thức tính lãi kép, lương 2 năm tiếp theo công nhân đó nhận được: T₂ = 24.8.10⁶.(1 + 10%)¹ = 212,2.10⁶ (đồng)

Lương 2 năm cuối cùng công nhân đó nhận được: T₃ = 24.8.10⁶.(1 + 10%)² = 232,32.10⁶(đồng)

Tổng số tiền T (đồng) kỹ sư đó nhận được sau 6 năm làm việc:

T = T₁ + T₂ + T₃ = 635 520 000 (đồng).

Câu 5: Anh Hưng đi làm được lĩnh lương khởi điểm 4 000 000 đồng/tháng. Cứ 3 năm, lương của anh Hưng lại được tăng thêm 7% /1 tháng. Hỏi sau 36 năm làm việc anh Hưng nhận được tất cả bao nhiêu tiền? (Kết quả làm tròn đến hàng nghìn đồng).

A. 1 287 968 000 đồng B. 1 931 953 000 đồng.

C. 2 575 937 000 đồng. D. 3 219 921 000 đồng.

Hướng dẫn giải

Chọn C.

Gọi a là số tiền lương khởi điểm, r là lương được tăng thêm.

+ Số tiền lương trong ba năm đầu tiên: 36a

+ Số tiền lương trong ba năm kế tiếp: 36[a + a.r] = 36a(1 + r)¹

+ Số tiền lương trong ba năm kế tiếp: 36a(1 + r)²

…

+ Số tiền lương trong ba năm cuối: 36a(1 + r)¹¹

Vậy sau 6 năm làm việc anh Hưng nhận được:

[1 + (1 + r)¹ + (1 + r)² + (1 + r)³ + .... + (1 + r)¹¹].a.36 = 2575936983 ≅ 2575937000 đồng.

Câu 6: Một người đem gửi tiền tiết kiệm vào một ngân hàng với lãi suất 1% một tháng. Biết rằng cứ sau mỗi quý (3 tháng) thì lãi sẽ được cộng dồn vào vốn gốc. Hỏi sau tối thiểu bao nhiêu năm thì người đó nhận lại được số tiền bao gồm cả vốn lẫn lãi gấp ba lần số tiền ban đầu

A. 8 . B. 9 . C. 10 . D. 11 .

Hướng dẫn giải

Chọn C.

Gọi a là số tiền người đó gửi ban đầu

Số tiền nhận được cả gốc lẫn lãi sau N năm là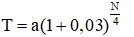

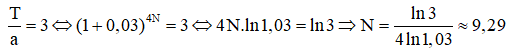
Câu 7: Một người vay ngân hàng một tỷ đồng theo phương thức trả góp để mua nhà. Nếu cuối mỗi tháng, bắt đầu từ tháng thứ nhất người đó trả 40 triệu đồng và chịu lãi số tiền chưa trả là 0,65% mỗi tháng (biết lãi suất không thay đổi) thì sau bao lâu người đó trả hết số tiền trên?

A. 29 tháng. B. 27 tháng.

C. 28 tháng. D. 26 tháng.

Hướng dẫn giải

Chọn D.

Gọi A là số tiền vay, a là số tiền gửi hàng tháng r là lãi suất mỗi tháng.

Đến cuối tháng thứ n thì số tiền còn nợ là:

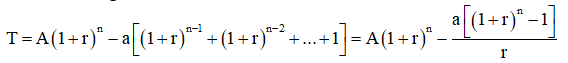
Hết nợ đồng nghĩa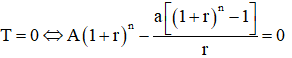

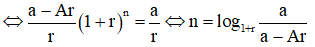
Áp dụng với A = 1 (tỷ), a = 0,04 (tỷ), r = 0,0065 ta được n ≈ 27,37.

Vậy cần trả 28 tháng.

Câu 8: Một người gửi ngân hàng 100 triệu theo thể thức lãi kép, lãi suất 0,5% một tháng. Sau ít nhất bao nhiêu tháng, người đó có nhiều hơn 125 triệu?

A. 45 tháng. B. 46 tháng. C. 44 tháng. D. 47 tháng.

Hướng dẫn giải:

Chọn B.

Sau 2 tháng, người đó nhận được 100 + 100.0,5% (triệu đồng) = 100.1,005¹ triệu đồng.

Sau 2 tháng, người đó nhận được:

100.1,005 + 100.1,005.0,005 = 100.1,005(1 + 0,005) = 100.(1,005)² triệu đồng

Sau n tháng, người đó nhận được: 100.(1,005)ⁿ triệu đồng.

Theo đề: 100.(1,005)ⁿ > 125 ⇔ n > log_1,0051,25 = 44,7 tháng.

Vậy sau 45 tháng, người đó có nhiều hơn 125 triệu đồng.

Câu 9: Năm 2014, một người đã tiết kiệm được x triệu đồng và dùng số tiền đó để mua nhà nhưng trên thực tế người đó phải cần 1,55x triệu đồng. Người đó quyết định gửi tiết kiệm vào ngân hàng với lãi suất là 6,9% / năm theo hình thức lãi kép và không rút trước kỳ hạn. Hỏi năm nào người đó mua được căn nhà đó (giả sử rằng giá bán căn nhà đó không thay đổi).

A. Năm 2019. B. Năm 2020.

C. Năm 2021. D. Năm 2022.

Hướng dẫn giải

Chọn C.

Số tiền người gửi tiết kiệm sau n năm là x(1 + 6,9%)ⁿ

Ta cần tìm n để x(1 + 6,9%)ⁿ = 1,55x ⇔ (1 + 6,9%)ⁿ = 1,55 ⇔ n ≈ 6,56....

Do đó, người gửi tiết kiệm cần gửi trọn 7 kỳ hạn, tức là 7 năm.

Vậy đến năm 2021 người đó sẽ có đủ tiền cần thiết.

Câu 10: Một người gửi ngân hàng 100 triệu đồng theo hình thức lãi kép, lãi suất 0,5% một tháng (kể từ tháng thứ 2, tiền lãi được tính theo phần trăm tổng tiền có được của tháng trước đó và tiền lãi của tháng sau đó). Hỏi sau ít nhất bao nhiêu tháng, người đó có nhiều hơn 125 triệu đồng?

A. 47 tháng. B. 45 tháng. C. 46 tháng. D. 44 tháng.

Hướng dẫn giải

Chọn C.

- Số tiền cả vốn lẫn lãi người gởi có sau n tháng là (triệu đồng) .

- Để có số tiền S = 125 (triệu đồng) thì phải sau thời gian

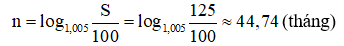
- Vậy: sau ít nhất 45 tháng người đó có nhiều hơn 125 triệu đồng.

III. BÀI TẬP TỰ LUYỆN

Câu 1: Ông Nam gởi 100 triệu đồng vào ngân hàng theo thể thức lãi kép kì hạn 1 năm với lãi suất là 12% một năm. Sau n năm ông Nam rút toàn bộ số tiền (cả vốn lẫn lãi). Tìm số nguyên dương n nhỏ nhất để số tiền lãi nhận được lớn hơn 40 triệu đồng (giả sử lãi suất hàng năm không thay đổi)

A. 4 . B. 5 . C. 2 . D. 3 .

Câu 2: Bạn Hùng trúng tuyển vào trường đại học A nhưng vì do không đủ nộp học phí nên Hùng quyết định vay ngân hàng trong 4 năm mỗi năm vay 3.000.000 đồng để nộp học phí với lãi suất 3%/năm. Sau khi tốt nghiệp đại học bạn Hùng phải trả góp hàng tháng số tiền T (không đổi) cùng với lãi suất 0,25%/tháng trong vòng 5 năm. Số tiền T hàng tháng mà bạn Hùng phải trả cho ngân hàng (làm tròn đến kết quả hàng đơn vị) là:

A. 232518 đồng. B. 309604 đồng. C. 215456 đồng. D. 232289 đồng.

Câu 3: Một người gửi tiết kiệm với lãi suất 6,5% năm và lãi hàng năm được nhập vào vốn. Hỏi khoảng bao nhiêu năm người đó thu được gấp đôi số tiền ban đầu?

A. 11 năm. B. 9 năm. C. 8 năm. D. 12 năm.

Câu 4: Một người gửi ngân hàng 100 triệu đồng theo hình thức lãi kép, lãi suất một tháng (kể từ tháng thứ 2, tiền lãi được tính theo phần trăm tổng tiền có được của tháng trước đó và tiền lãi của tháng trước đó). Sau ít nhất bao nhiêu tháng, người đó có nhiều hơn 125 triệu.

A. 45 tháng. B. 47 tháng. C. 44 tháng. D. 46 tháng.

Câu 5: Một người gửi 10 triệu đồng vào ngận hàng trong thời gian 10 năm với lãi suất 5% năm. Hỏi người đó nhận được số tiền nhiều hơn hay ít hơn bao nhiêu nếu ngân hàng trả lại suất 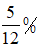tháng ?

A. Nhiều hơn. B. Ít hơn. C. Không thay đổi. D. Không tính được.

Câu 6: Một người gửi tiết kiệm vào ngân hàng A với số tiền là 100 triệu đồng với lãi suất mỗi quý (3 tháng) là 2,1%. Số tiền lãi được cộng vào vốn sau mỗi quý. Sau 2 năm người đó vẫn tiếp tục gửi tiết kiệm số tiền thu được từ trên nhưng với lãi suất 1,1% mỗi tháng. Số tiền lãi được cộng vào vốn sau mỗi tháng. Hỏi sau 3 năm kể từ ngày gửi tiết kiệm vào ngân hàng A người đó thu được số tiền gần nhất với giá trị nào sau đây?

A. 134,65 triệu đồng. B. 130,1 triệu đồng.

C. 156,25 triệu đồng. D. 140,2 triệu đồng.

Câu 7: Ông A gửi số tiền 100 triệu đồng vào ngân hàng với lãi suất 7% trên năm, biết rằng nếu không rút tiền ra khỏi ngân hàng thì cứ sau mỗi năm số tiền lãi sẽ được nhập vào vốn ban đầu. sau thời gian 10 năm nếu không rút lãi lần nào thì số tiền mà ông A nhận được tính cả gốc lẫn lãi là

A. 10⁸.(1 + 0,07)¹⁰ B. 10⁸.0,07¹⁰ C. 10⁸.(1 + 0,7)¹⁰ D. 10⁸.(1 + 0,007)¹⁰

Câu 8: Ông Nam gửi 100 triệu đồng vào ngân hàng theo thể thức lãi kép kì hạn một năm với lãi suất là 12% một năm. Sau n năm ông Nam rút toàn bộ tiền (cả vốn lẫn lãi). Tìm n nguyên dương nhỏ nhất để số tiền lãi nhận được hơn 40 triệu đồng. (Giả sử rằng lãi suất hàng năm không thay đổi).

A. 5 . B. 2 . C. 4 . D. 3 .

Câu 9: Ông An bắt đầu đi làm với mức lương khởi điểm là 1 triệu đồng một tháng. Cứ sau 3 năm thì ông An được tăng lương 4-%. Hỏi sau tròn 20 năm đi làm tổng tiền lương ông An nhận được là bao nhiêu (làm tròn đến hai chữ số thập phân sau dấu phẩy)?

A. 726,74 triệu. B. 71674 triệu. C. 858,72 triệu. D. 768,37 triệu.

Câu 10: Giả sử vào cuối năm thì một đơn vị tiền tệ mất 10% giá trị so với đầu năm. Tìm số nguyên dương nhỏ nhất sao cho sau n năm, đơn vị tiền tệ sẽ mất đi ít nhất 90% giá trị của nó?

A. 16 B. 18. C. 20. D. 22.

ĐÁP ÁN

1D

2D

3A

4A

5A

6A

7A

8D

9D

10D