Biết z1; z2 là số phức thỏa điều kiện z^2 - |z|^2 + 1 = 0
Câu hỏi:
Biết z1; z2 là số phức thỏa điều kiện z2 - |z|2 + 1 = 0. Tính 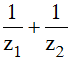
A. –i
B. i
C. 1 + i
D. 0
Trả lời:
Chọn D.
Đặt z = x + yi. Phương trình z2 - |z|2 + 1 = 0 trở thành:
x2 - y2 + 2xyi - ( x2 + y2) + 1 = 0
Suy ra: -2y2 + 1+ 2xyi = 0
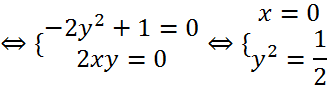

Vậy số phức z cần tìm là:  .Suy ra
.Suy ra 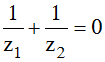
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Biết z1; z2 là các số phức thỏa mãn điều kiện 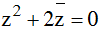 . Tìm |z1 + z2|
. Tìm |z1 + z2|
Xem lời giải »
Câu 2:
Biết z1; z2; z3; z4 là các số phức thỏa điều kiện 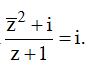 .
.
Tính | z1| + | z2| + | z3| + | z4|
Xem lời giải »
Câu 3:
Cho số phức z thỏa điều kiện 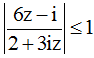 . Tìm khẳng định đúng
. Tìm khẳng định đúng
Xem lời giải »
Câu 4:
Gọi z là số phức khác 0 sao cho 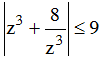 .Tìm khẳng định đúng
.Tìm khẳng định đúng
Xem lời giải »
Câu 5:
Cho phương trình z2 + mz - 6i = 0. Để phương trình có tổng bình phương hai nghiệm bằng 5 thì m có dạng m = ± ( a + bi). Giá trị a + 2b là:
Xem lời giải »
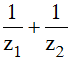
.Suy ra

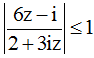 . Tìm khẳng định đúng
. Tìm khẳng định đúng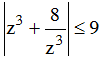 .Tìm khẳng định đúng
.Tìm khẳng định đúng