Cách biến đổi đẳng thức đã cho thành đẳng thức logarit cực hay - Toán lớp 12

Cách biến đổi đẳng thức đã cho thành đẳng thức logarit cực hay

Với Cách biến đổi đẳng thức đã cho thành đẳng thức logarit cực hay Toán lớp 12 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập biến đổi đẳng thức đã cho thành đẳng thức logarit từ đó đạt điểm cao trong bài thi môn Toán lớp 12.

1. Phương pháp giải

Từ đẳng thức đã cho thêm bớt thích hợp để xuất hiện hằng đẳng thức. Sau đó, lấy loga 2 vế ( lựa chọn cơ số thích hợp- dựa vào đáp án) ...,đồng thời áp dụng các tính chất của logarit..

2. Ví dụ minh họa

Ví dụ 1. Cho a > 0; b > 0 thỏa điều kiện a² + b² = 7ab .Khẳng định nào sau đây đúng:

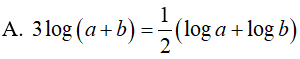
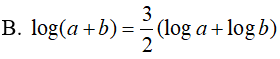
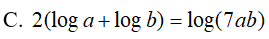
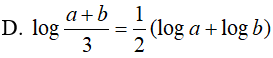
Lời giải:

Đáp án: D

Theo giả thiết: a² + b² = 7ab ⇔ (a + b)² = 9ab ( cộng 2ab vào 2 vế).

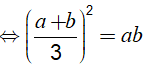
Lấy logarit cơ số 10 hai vế ta được:

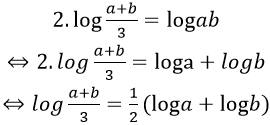
Ví dụ 2. Cho x; y là các số thực lớn hơn 1 thoả mãn x² + 9y² = 6xy. Tính

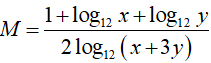
Lời giải:

Đáp án: B

* Ta có x² + 9y² = 6xy ⇔ x² − 6xy + 9y² = 0

⇔ (x − 3y)² = 0 ⇔ x = 3y.

Khi đó

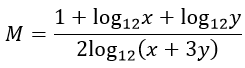
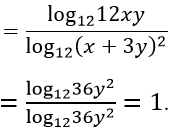
Ví dụ 3. Cho a, b là các số thực dương khác 1, thoả mãn log_a²b + log_b²a = 1 . Mệnh đề nào dưới đây là đúng?

Lời giải:

Đáp án: B

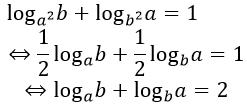
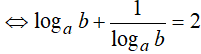
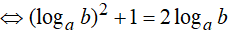
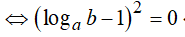
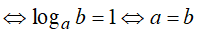
Ví dụ 4. Cho các số dương a, b thõa mãn 4a² + 9b² = 13ab. Chọn câu trả lời đúng

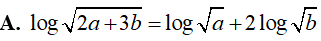
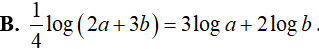
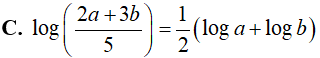
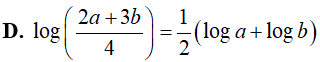
Lời giải:

Đáp án: C

Ta có: 4a² + 9b² = 13ab ⇔ 4a² + 12ab + 9b² = 25ab

⇔ (2a + 3b)² = 25ab ( vì a; b > 0 nên a + b > 0; ab > 0 ).

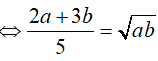
Suy ra

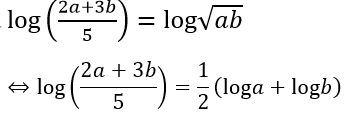
Ví dụ 5. Cho x, y > 0 và x² + 4y² = 12xy. Khẳng định nào sau đây là khẳng định đúng?

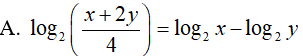
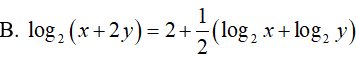
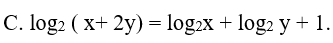
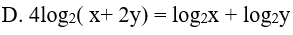
Lời giải:

Đáp án: B

Vì x² + 4y² = 12xy nên x² + 4xy + 4y² = 16xy

⇔ (x + 2y)² = 16xy ⇔ log₂ (x + 2y)² = log₂16xy.

⇔ 2. log₂ (x + 2y) = log₂ 16 + log₂ x + log₂ y

⇔ 2.log₂ ( x + 2y ) = 4 + log₂x + log₂y

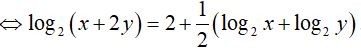
Ví dụ 6. Cho a, b là các số thực dương thoả mãn a² + b² = 14ab. Khẳng định nào sau đây là sai ?

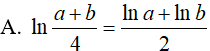
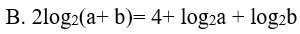
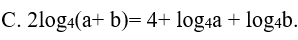
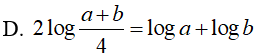
Lời giải:

Đáp án: C

Ta có

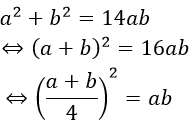
Nên ta có 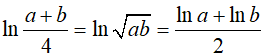vậy A đúng

2log₂ (a+b) = log₂ (a+b)² = log₂ (16ab)=4 + log₂a + log₂b vậy B đúng

2log₄ (a+b) = log₄ (a+b)² = log₄ (16ab)=2 +l og₄a + log₄b vậy C sai

vậy D đúng