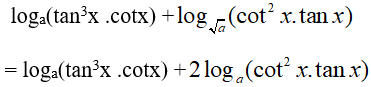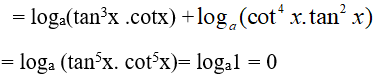Bài tập Tính giá trị của biểu thức logarit cực hay - Toán lớp 12

Bài tập Tính giá trị của biểu thức logarit cực hay

Với Bài tập Tính giá trị của biểu thức logarit cực hay Toán lớp 12 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Tính giá trị của biểu thức logarit từ đó đạt điểm cao trong bài thi môn Toán lớp 12.

1. Phương pháp giải

* Để tính giá trị của một biểu thức chứa logarit ta cần sử dụng các quy tắc tính logarit và đổi cơ số của logarit.

* Các quy tắc tính logarit :

Cho 3 số dương a , b và c với a ≠ 1 , ta có

log_a(bc) = log_ab + log_ac

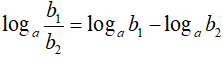
Đặc biệt : với a, b > 0; a ≠ 1 thì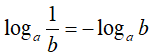

log_ab^α = αlog_ab

Đặc biệt: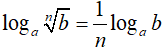

* Đổi cơ số của lôgarit

Cho 3 số dương a, b, c với a ≠ 1,c ≠ 1 ta có

• hay log_ca. log_ab = log_c b

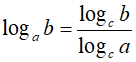
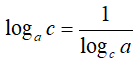
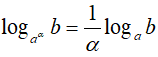
• Đặc biệt: và với α ≠ 0.

2. Ví dụ minh họa

Ví dụ 1. Cho a > 0,a ≠ 1 giá trị của biểu thức a^log_√a16 bằng bao nhiêu ?

A. 16    B. 4    C. 32    D. 256

Lời giải:

Đáp án: D

Ta có:

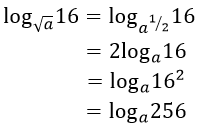
Do đó

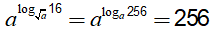
Ví dụ 2. Giá trị của biểu thức A = log₂12 + 2log₂5 − log₂15 − log₂150 bằng:

Lời giải:

Đáp án: B

Ta có: A = log₂12 + 2log₂5 − log₂15 − log₂150

= log₂12 + log₂5² − log₂15 − log₂150

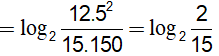
Ví dụ 3. Cho a > 0, tính 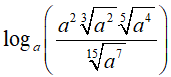bằng:

Lời giải:

Đáp án: A

Ta có:

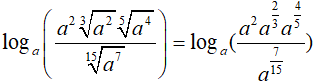
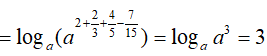
Ví dụ 4. Cho số dương a khác 1. Tính giá trị biểu thức A = a^6log_a352 có giá trị bằng bao nhiêu?

A. 25    B. 625    C. 5    D. 125

Lời giải:

Đáp án: B

Ta có:

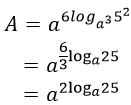
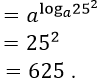
Ví dụ 5. Tính giá trị biểu thức .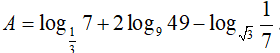

A. A=3log₃7.    B. A = log₃7.    C. A = 2log₃7.    D. A = 4log₃7.

Lời giải:

Đáp án: A

Ta có:

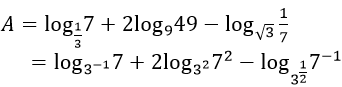
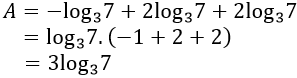
Ví dụ 6. Biểu thức 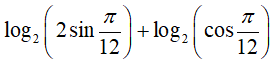có giá trị bằng:

A. −1    B. −2    C. 1    D. log₂3.

Lời giải:

Đáp án: A

Ta có:

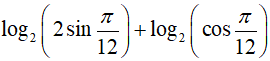
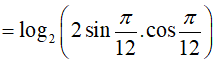
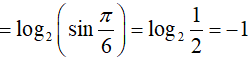
Ví dụ 7. Cho số thực a > 0 và a khác 1; 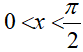. Tính log_a(tan³x.cotx) + log_√a(cot²x . tanx) ?

A. 1    B. −1    C. 0    D. 2

Lời giải:

Đáp án: C

Ta có: