Cách so sánh biểu thức chứa logarit cực hay - Toán lớp 12

Cách so sánh biểu thức chứa logarit cực hay

Với Cách so sánh biểu thức chứa logarit cực hay Toán lớp 12 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập so sánh biểu thức chứa logarit từ đó đạt điểm cao trong bài thi môn Toán lớp 12.

1. Phương pháp giải

Cho số dương a khác 1 và hai số dương b, c.

• Khi a > 1 thì log_ab > log_ac ⇔ b > c.

• Khi 0 < a < 1 thì log_ab > log_ac ⇔ b < c.

Ngoài ra, cần sử dụng các công thức quy tắc tính logarit và đổi cơ số của logarit.

2. Ví dụ minh họa

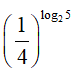
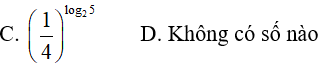
Ví dụ 1. Trong các số 3^log₃4; 3^2log₃2; những số nào nhỏ hơn 1

Lời giải:

Đáp án: C

Ta so sánh các số với 1

+ 3^log₃4 > 1.

+ 3^2log₃2 = 3^log₃22 = 4 > 1

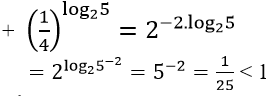
Ví dụ 2. Trong các số sau, số nào lớn nhất?

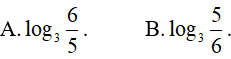
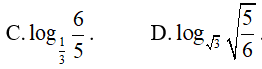
Lời giải:

Đáp án: A

Đưa về cùng 1 cơ số và so sánh:

Ta thấy

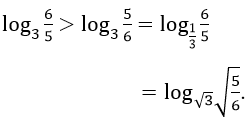
Ví dụ 3. Trong các số sau, số nào lớn nhất?

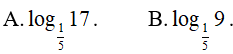
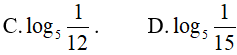
Lời giải:

Đáp án: A

Đưa về cùng 1 cơ số và so sánh:

Ta thấy

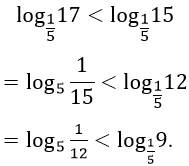
Ví dụ 4. Cho hai số thực a; b với 1 < a < b. Khẳng định nào sau đây là đúng:

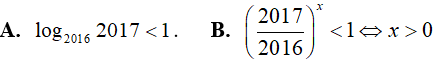
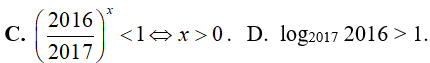
Lời giải:

Đáp án: C

Ta xét các phương án:

+ A sai vì log₂₀₁₆2017 > log₂₀₁₆2016 = 1.

+ B sai vì

+ C đúng vì 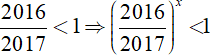với mọi x dương.

+ D sai vì log₂₀₁₇2016 < log₂₀₁₇2017 = 1.

Ví dụ 5. Cho hai số thực a, b với 1 < a < b. Khẳng định nào sau đây là khẳng định đúng?

A. log_ab < 1 < log_ba.    B. 1 < log_ab < log_ba .

C. log_ab < log_ba < 1.    D. log_ba < 1 < log_ab

Lời giải:

Đáp án: D

Từ giả thiết 1 < a < b nên ta có: log_a1 < log_aa < log_ab hay 0 < 1 < log_ab .

Áp dụng công thức đổi cơ số thì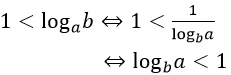

vì log_ba > 0 nên ta có log_ba < 1 < log_ab.

Ví dụ 6. Cho các số thực a ,b thỏa mãn a > b > 1. Chọn khẳng định sai trong các khẳng định sau:

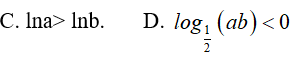
Lời giải:

Đáp án: A

Ta xét các phương án:

+ a > b > 1 => lna > lnb > 0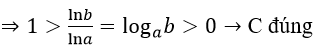

+ Do a > b > 1 nên:

1 > (log_ab)² => log_ab . log_ba > (log_ab)² => log_ba > log_ab -> B đúng

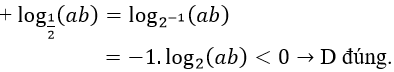
Do đó, phương án A sai.

Ví dụ 7. Cho hai số thực a, b với 1 < a < b. Khẳng định nào sau đây là khẳng định đúng?

A. log_ab < 1 < log_ba.    B. 1 < log_ab < log_ba.

C. log_ab < log_ba < 1    D. log_ba < 1 < log_ab

Lời giải:

Đáp án: D

Từ giả thiết 1 < a < b ta có: 0 < log_aa < log_ab ⇔ 1 < log_ab

Áp dụng công thức đổi cơ số thì:

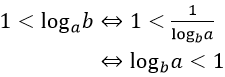
Vì log_ba > 0 nên ta có log_ba < 1 < log_ab.